Часові характеристики елементів (системи)

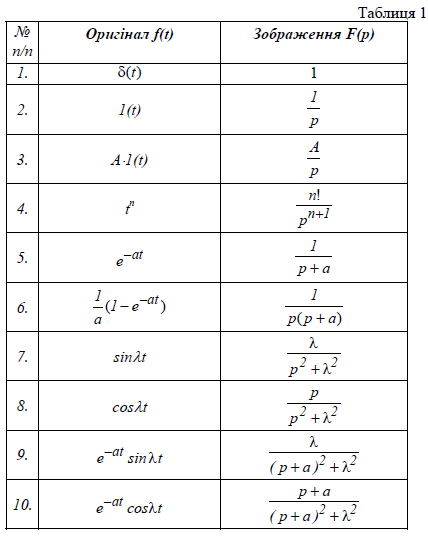
В таблиці 1 наведені оригінали і зображення Лапласа для деяких простих функцій, що найчастіше зустрічаються в задачах ТАК. В найпростішому випадку оригінал функції можна визначити за таблицею перетворень Лапласа, якщо зображення є табличним. Для розглядуваного прикладу ланки з передаточною функцією (4) перехідну функцію визначаємо з виразу: Для ланки з передаточною функцією (4) вираз для… Читати ще >
Часові характеристики елементів (системи) (реферат, курсова, диплом, контрольна)
Перехідна функція ланки h (t)
Перехідною функцією ланки (системи) h(t) зветься реакція ланки.
(системи) на одиничне ступінчасте діяння (мал. 3, а), тобто перехідний процес на виході xвих(t) за одиничного стрибка на вході xвх(t) за нульових початкових умов.
Перехідна функція h(t) може бути визначена вирішенням диференціального рівняння ланки (системи) звичайним або операційним методами. Для визначення h (t) операційним методом в рівнянні (3) підставимо зображення одиничної ступінчастої функції.
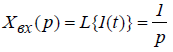
і знайдемо зображення перехідної функції:
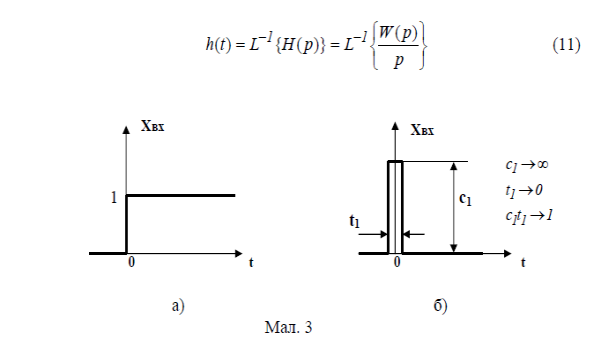
Для розглядуваного прикладу ланки з передаточною функцією (4) перехідну функцію визначаємо з виразу:
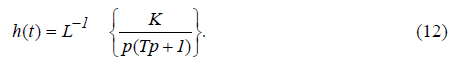
Методи визначення оригіналу функції за відомим її зображенням наведені в п. 2.3.
Імпульсна перехідна (вагова) функція ланки (системи) w (t)
Ваговою функцією w(t) зветься реакція ланки (системи) на одиничний імпульс (t)д на вході ланки (системи), тобто на миттєвий імпульс нескінченно великої амплітуди і одиничної площі (мал.3,б).
Оскільки одиничний імпульс д (t)може бути отриманий.

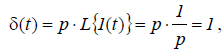
диференціюванням одиничного стрибка, або ж в операційній формі то зображення вагової функції ланки (системи) дорівнює відповідній передаточній функції:
L{w(t)}=W(p)?д (p) =W(p). (13).
Таким чином, щоб отримати вагову функцію w(t), треба знайти оригінал (обернене перетворення Лапласа), що відповідає передаточній функції:
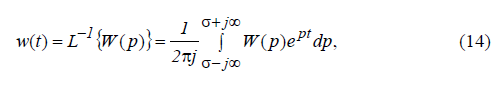
де L?1{*} знак оберненого перетворення Лапласа.
Для ланки з передаточною функцією (4) вираз для визначення вагової функції (14) запишемо у вигляді:

Визначення оригіналу функції за її зображенням (обернене перетворення Лапласа).
Розглянемо деякі способи оберненого перетворення Лапласа, які дозволяють на практиці досить просто визначати оригінал функції за її зображенням, тобто такі, що є простими інженерними методами визначення перехідної h (t) і вагової w (t) функцій ланки (системи) за відомою передаточною функцією W (p).
1. В найпростішому випадку оригінал функції можна визначити за таблицею перетворень Лапласа, якщо зображення є табличним.
В таблиці 1 наведені оригінали і зображення Лапласа для деяких простих функцій, що найчастіше зустрічаються в задачах ТАК.
2. Якщо зображення за Лапласом є дробово-раціональною функцією р, то таку функцію можна розкласти на елементарні дроби і, скориставшись теоремою про додавання, обмежитись оберненим перетворенням Лапласа елементарних зображень, наведених в табл. 1.