Розрахунок елементів дерев'яних конструкцій

Расчет внецентренно-растянутых и растянуто-изгибаемых элементов следует производить по формуле.

(27).

где W_расч — расчетный момент сопротивления поперечного сечения (см. п. 4.9);

F_расч — площадь расчетного сечения нетто.

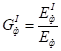
Для древесины из однонаправленного шпона в формуле (27) следует использовать соответствующие значения расчетных сопротивлений.

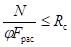
Расчет на прочность внецентренно-сжатых и сжато-изгибаемых элементов следует производить по формуле.

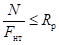
(или? R^с_д.ш), (28).

где М_д — изгибающий момент от действия поперечных и продольных нагрузок, определяемый из расчета по деформированной схеме.

Примечания.

1 Для шарнирно-опертых элементов при симметричных эпюрах изгибающих моментов синусоидального, параболического, полигонального и близких к ним очертаний, а также для консольных элементов М_д следует определять по формуле.

(29).

где о — коэффициент, изменяющийся от 1 до 0, учитывающий дополнительный момент от продольной силы вследствие прогиба элемента, определяемый по формуле.

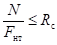
(30).

для древесины из однонаправленного шпона.

.

М — изгибающий момент в расчетном сечении без учета дополнительного момента от продольной силы;

ц — коэффициент, определяемый по формуле (8).

2 В случаях когда в шарнирно-опертых элементах эпюры изгибающих моментов имеют треугольное или прямоугольное очертание, коэффициент по формуле (30) следует умножать на поправочный коэффициент k_н.

(31).

где _н — коэффициент, который следует принимать равным 1,22 при эпюрах изгибающих моментов треугольного очертания (от сосредоточенной силы) и 0,81 — при эпюрах прямоугольного очертания (от постоянного изгибающего момента).

3 При несимметричном загружении шарнирно-опертых элементов величину изгибающего момента М_д следует определять по формуле.

(32).

где М_с и М_к — изгибающие моменты в расчетном сечении элемента от симметричной и кососимметричной составляющих нагрузки;

о_с и о_к — коэффициенты, определяемые по формуле (30) при величине гибкости, соответствующей симметричной и кососимметричной формам продольного изгиба.

• 4 Для элементов, переменных по высоте сечения, площадь F_бр в формуле (30) следует принимать для максимального по высоте сечения, а коэффициент ц следует умножать на коэффициент k_жN, принимаемый по таблице Г. 1 приложения Г.
• 5 При отношении напряжений от изгиба к напряжениям от сжатия менее 0,1 сжато-изгибаемые элементы следует проверять также на устойчивость по формуле (6) без учета изгибающего момента.

Расчет на устойчивость плоской формы деформирования сжато-изгибаемых элементов следует производить по формуле.

(33).

где F_бр — площадь брутто с максимальными размерами сечения элемента на участке l_p;

W_бр — см. п. 4.14;

n = 2 — для элементов без закрепления растянутой зоны из плоскости деформирования и n = 1 для элементов, имеющих такие закрепления;

ц — коэффициент продольного изгиба, определяемый по формуле (8) для гибкости участка элемента расчетной длиной l_p из плоскости деформирования;

ц_м — коэффициент, определяемый по формуле (23).

Для древесины из однонаправленного шпона следует принимать соответствующие значения расчетных сопротивлений по п. 3.6.

При наличии в элементе на участке l_p закреплений из плоскости деформирования со стороны растянутой от момента М кромки коэффициент ц_м следует умножать на коэффициент k_пМ, определяемый по формуле (24), а коэффициент ц — на коэффициент k_пN пo формуле.

(34).

где б_р, l_p, h, m — см. п. 4.14.

При расчете элементов переменного по высоте сечения, не имеющих закреплений из плоскости по растянутой от момента М кромке, или при m < 4 коэффициенты ц и ц_м, определяемые по формулам (8) и (23), следует дополнительно умножать соответственно на коэффициенты k_жN и k_жМ, приведенные в таблицах Г. 1 и Г. 2 приложения Г.

При m? 4 k_жN = k_жМ = 1.

В составных сжато-изгибаемых элементах следует проверять устойчивость наиболее напряженной ветви, если расчетная длина ее превышает семикратную толщину ветви, по формуле.

(35).

где ц₁ — коэффициент продольного изгиба для отдельной ветви, вычисленный по ее расчетной длине l₀ (см. п. 4.6);

F_бр, W_бр — площадь и момент сопротивления брутто поперечного сечения элемента.

Устойчивость сжато-изгибаемого составного элемента из плоскости изгиба следует проверять по формуле (6) без учета изгибающего момента.

Число срезов связей n_с, равномерно расставленных в каждом шве сжато-изгибаемого составного элемента на участке с однозначной эпюрой поперечных сил при приложении сжимающей силы по всему сечению, должно удовлетворять условию.

(36).

где S_бр — статический момент брутто сдвигаемой части поперечного сечения относительно нейтральной оси;

I_бр — момент инерции брутто поперечного сечения элемента;

Т — расчетная несущая способность одной связи в данном шве;

М_д — изгибающий момент, определяемый по п. 4.17.

Расчетные длины и предельные гибкости элементов деревянных конструкций Для определения расчетной длины прямолинейных элементов, загруженных продольными силами по концам, коэффициент м₀ следует принимать равным:

при шарнирно-закрепленных концах, а также при шарнирном закреплении в промежуточных точках элемента — 1;

при одном шарнирно-закрепленном и другом защемленном конце — 0,8;

при одном защемленном и другом свободном нагруженном конце — 2,2;

при обоих защемленных концах — 0,65.

В случае равномерно распределенной по длине элемента продольной нагрузки коэффициент м₀ следует принимать равным:

при обоих шарнирно-закрепленных концах — 0,73;

при одном защемленном и другом свободном конце — 1,2.

Расчетную длину пересекающихся элементов, соединенных между собой в месте пересечения, следует принимать равной:

при проверке устойчивости в плоскости конструкций — расстоянию от центра узла до точки пересечения элементов;

при проверке устойчивости из плоскости конструкции:

• а) в случае пересечения двух сжатых элементов — полной длине элемента;
• б) в случае пересечения сжатого элемента с неработающим — величине l₁ умноженной на коэффициент м₀:

(37).

где l₁, л₁, F₁ — полная длина, гибкость и площадь поперечного сечения сжатого элемента;

l₂, л₂, F₂ — длина, гибкость и площадь поперечного сечения неработающего элемента.

Величину м₀ следует принимать не менее 0,5;

в) в случае пересечения сжатого элемента с элементом, растянутым равной по величине силой, — наибольшей длине сжатого элемента, измеряемой от центра узла до точки пересечения элементов.

Если пересекающиеся элементы имеют составное сечение, то в формулу (37) следует подставлять соответствующие значения гибкости, определяемые по формуле (11).

Гибкость элементов и их отдельных ветвей в деревянных конструкциях не должна превышать значений, указанных в таблице 14.

Таблица 14.

Особенности расчета клееных элементов из фанеры с древесиной Расчет клееных элементов из фанеры с древесиной следует выполнять по методу приведенного поперечного сечения.

Прочность растянутой фанерной обшивки плит (рисунок 3) и панелей следует проверять по формуле.

(38).

где М — расчетный изгибающий момент;

R_ф.р — расчетное сопротивление фанеры растяжению;

m_ф — коэффициент, учитывающий снижение расчетного сопротивления в стыках фанерной обшивки, принимаемый равным при усовом соединении или с двусторонними накладками: m_ф = 0,6 для фанеры обычной и m_ф = 0,8 для фанеры бакелизирован-ной; при отсутствии стыков m_ф = 1;

W_пр — момент сопротивления поперечного сечения, приведенного к фанере, который следует определять в соответствии с указаниями п. 4.25.

1 — продольные ребра; 2 — обшивка.

Рисунок 3 — Поперечное сечение клееных плит из фанеры и древесины Приведенный момент сопротивления поперечного сечения клееных элементов из фанеры с древесиной следует определять по формуле.

(39).

где у₀ — расстояние от центра тяжести приведенного сечения до нижней грани обшивки;

I_пр — момент инерции сечения, приведенного к фанере.

(40).

где I_ф — момент инерции поперечного сечения фанерных обшивок;

I — момент инерции поперечного сечения деревянных ребер каркаса;

Е/Е_ф — отношение модулей упругости древесины и фанеры.

При определении приведенных моментов инерции и приведенных моментов сопротивления расчетную ширину фанерных обшивок следует принимать равной b_рас = 0,9b при l? 6а и b_рас = 0,15a^-1b при l < 6а (b — полная ширина сечения плиты, l — пролет плиты, а — расстояние между продольными ребрами по осям).

Устойчивость сжатой обшивки плит и панелей следует проверять по формуле.

(41).

где ;

(а — расстояние между ребрами в свету; д — толщина фанеры).

Верхнюю обшивку плит дополнительно следует проверять на местный изгиб от сосредоточенного груза Р = 1 кН (100 кгс) (с коэффициентом перегрузки n = 1,2) как заделанную в местах приклеивания к ребрам пластинку.

Проверку на скалывание ребер каркаса плит и панелей или обшивки по шву в месте примыкания ее к ребрам следует производить по формуле.

(42).

где Q — расчетная поперечная сила;

S_пр — статический момент сдвигаемой части приведенного сечения относительно нейтральной оси;

R_ск — расчетное сопротивление скалыванию древесины вдоль волокон или фанеры вдоль волокон наружных слоев;

b — расчетная ширина сечения, которую следует принимать равной суммарной ширине ребер каркаса.

4.28 Расчет на прочность поясов изгибаемых элементов двутаврового и коробчатого сечений с фанерными стенками (рисунок 4) следует производить по формуле (17), принимая Wрас = Wпр, при этом напряжения в растянутом поясе не должны превышать Rр, а в сжатом — цRс (ц — коэффициент продольного изгиба из плоскости изгиба).

а — двутавровое сечение; б — коробчатое сечение.

Рисунок 4 — Поперечные сечения клееных балок с плоской фанерной стенкой При проверке стенки на срез по нейтральной оси в формуле (42) значение R_ск принимается равным R_ф.ср, а расчетная ширина b_pac равна:

(43).

где Уд_ст — суммарная толщина стенок.

При проверке скалывания по швам между поясами и стенкой в формуле (42) R_ск = R_ф.ск, а расчетную ширину сечения следует принимать равной:

(44).

где h_п — высота поясов;

п — число вертикальных швов.

Прочность стенки в опасном сечении на действие главных растягивающих напряжений в изгибаемых элементах двутаврового и коробчатого сечений следует проверять по формуле.

(45).

где R_ф.р. — расчетное сопротивление фанеры растяжению под углом, определяемое по графику рисунка Д. 1 приложения Д;

у_ст — нормальное напряжение в стенке от изгиба на уровне внутренней кромки поясов;

ф_ст — касательные напряжения в стенке на уровне внутренней кромки поясов;

— угол, определяемый из зависимости.

. (46).

Устойчивость стенки с продольным по отношению к оси элемента расположением волокон наружных слоев следует проверять на действие касательных и нормальных напряжений при условии.

(47).

где h_ст — высота стенки между внутренними гранями полок;

д — толщина стенки.

Расчет следует производить по формуле.

(48).

где k_и и k_ф — коэффициенты, определяемые по графикам рисунков Д. 2 и Д. 3 приложения Д;

h_рас — расчетная высота стенки, которую следует принимать равной h_ст при расстоянии между ребрами а? h_ст и равной а при а < h_ст.

При поперечном по отношению к оси элемента расположении наружных волокон фанерной стенки проверку устойчивости следует производить по формуле (48) на действие только касательных напряжений в тех случаях, когда.

. (49).

Расчет элементов деревянных конструкций по предельным состояниям второй группы Деформации деревянных конструкций или их отдельных элементов следует определять с учетом сдвига и податливости соединений. Величину деформаций податливого соединения при полном использовании его несущей способности следует принимать по таблице 15, а при неполном — пропорциональной действующему на соединение усилию.

Таблица 15.

Прогибы и перемещения элементов конструкций не должны превышать предельных, установленных СНиП 2.01.07 и таблицей 16.

Прогиб изгибаемых элементов следует определять по моменту инерции поперечного сечения брутто. Для составных сечений момент инерции умножается на коэффициент k_ж, учитывающий сдвиг податливых соединений и приведенный в таблице 13.

Таблица 16.

Наибольший прогиб шарнирно-опертых и консольных изгибаемых элементов постоянного и переменного сечений f следует определять по формуле.

(50).

где f₀ — прогиб балки постоянного сечения высотой h без учета деформаций сдвига;

h — наибольшая высота сечения;

l — пролет балки;

k — коэффициент, учитывающий влияние переменности высоты сечения, принимаемый равным 1 для балок постоянного сечения;

с — коэффициент, учитывающий влияние деформаций сдвига от поперечной силы.

Значения коэффициентов k и с для основных расчетных схем балок приведены в таблице Г. 3 приложения Г.

Прогиб клееных элементов из фанеры с древесиной следует определять, принимая жесткость сечения равной 0,7EI_пр. Расчетная ширина обшивок плит и панелей при определении прогиба принимается в соответствии с указаниями п. 4.25.

Прогиб сжато-изгибаемых шарнирно-опертых симметрично нагруженных элементов и консольных элементов следует определять по формуле.

(51).

где f — прогиб, определяемый по формуле (50);

о — коэффициент, определяемый по формуле (30).

Особенности расчета балок композитного сечения Изгибающие моменты, усилия и напряжения в элементах композитной балки следует, в общем случае, определять суммированием силовых факторов, возникающих на различных стадиях и этапах работы, соответствующих условиям возведения и загружения конструкции.

Для нахождения изгибающих моментов, сдвигающих и отрывающих усилий между железобетоном и деревом, внутренних напряжений, а также при определении общих деформаций работа бетона принимается, как правило, упругой, независимо от величины и знака напряжений в бетоне. При этом в необходимых случаях учитывается ползучесть бетона.

В расчетах композитных балок, выполняемых в предположении упругости бетона, следует использовать приведенные к древесине геометрические характеристики поперечных сечений этих балок.

(52).

где Е_b — модуль упругости железобетона;

Е — модуль упругости древесины вдоль волокон.

Высота деревянного ребра принимается равной:

• (1/15−1/25)l — для разрезных балок;
• (1/20−1/30)l — для неразрезных балок, где l — пролет балок.

Толщина железобетонной плиты принимается равной 80−150 мм. Угол наклона вклеенных анкеров = 30−45°.

Расстояния между осями вклеенных анкеров вдоль волокон (см. рисунок 17) следует принимать не менее:

S₁ = 14d при = 30°;

S₂= 10d при = 45°.

Расстояние от оси анкера до торца по направлению волокон следует принимать не менее 5d.

Расстояния в направлении поперек волокон следует принимать:

S₂? 3d — между осями анкеров;

S₃? 2d, но не менее 30 мм — от оси анкера до кромки.

• 4.38 Расчет ведется в 2 стадии:
• 1-я стадия — расчет деревянного ребра на вес железобетонной плиты;
• 2-я стадия — расчет на постоянные и временные нагрузки.

Напряжения по нижней грани деревянного ребра проверяют по формуле.

(53).

где — напряжение в ребре на первой стадии;

— напряжение в ребре на второй стадии;

М₁ — изгибающий момент от веса железобетонной плиты;

М₂ — изгибающий момент от расчетной нагрузки (кроме веса железобетонной плиты);

W_д — момент сопротивления деревянного ребра;

— момент сопротивления композитного сечения, приведенного к древесине;

у — расстояние от нейтральной оси приведенного сечения по нижней грани балки.

Напряжения по верхней грани железобетонной плиты проверяют по формуле.

(54).

где W_b.пр — момент сопротивления композитного сечения, приведенного к бетону;

R_b — расчетное сопротивление бетона растяжению.

Расчетная ширина железобетонной плиты принимается равной расстоянию между ребрами, но не более 1/6 пролета. При толщине плиты менее 1/10 высоты композитной балки расчетная ширина свеса принимается не более 6-кратной толщины плиты.

Требуемое число анкеров определяется из расчета на сдвиг по плоскости скалывания плиты и ребер.

Несущая способность одного анкера на сдвиг определяется по формуле.

(55).

где F_а — площадь поперечного сечения анкера;

R_а — расчетное сопротивление материала анкера на растяжение;

d — номинальный диаметр анкера;

R_b — расчетное сопротивление бетона на осевое сжатие (призменная прочность).