Контрольний приклад. 
Програмна інженерія

Значення всіх навчальних параметрів представлені у формі «Да-Ні». Навчальна вибірка складається з 31 прикладу, кожен з яких представляє собою ситуацію виборів, починаючи з 1864 року (табл. 6.1), де відповіді «Так» позначені одиницями, а відповіді «Ні» — нулями.

Питання:

• 1. У рік виборів була активна третя партія?
• 2. Була серйозна конкуренція при висуненні кандидата від правлячої партії?
• 3. Чи був рік виборів часом спаду або депресії?
• 4. Правлячий президент здійснив істотні зміни в політиці?
• 5. Під час правління були істотні соціальні хвилювання?

Клас 1 означає, що в даній ситуації був обраний кандидат правлячої партії, клас 2 — кандидат опозиційної партії. Після навчання мережа повинна передбачити відповідь для ситуації, відображеної в табл. 6.2, яка не входила в навчальну вибірку (результат цих виборів відомий — в 1992 році президентом став Б. Клінтон).

Таблица 6.1 — Навчальна вибірка.

Популярність генетичних алгоритмів обумовлена тим, що вони дозволяють знайти більш гарні або «раціональні» рішення NP-повних практичних задач оптимізації за менший час, ніж інші методи, які застосовуються у цих випадках. Звичайно ж, термін «гарні» або «раціональні» не є строгим в математичному значенні.

Під «раціональними» маються на увазі рішення, які задовольняють дослідника. Адже в більшості реальних задач немає необхідності знаходити саме глобальний оптимум. Найчастіше метою пошуку є рішення, які задовольняють певним обмеженням. Наприклад, час іспитів обладнання не повинен перевищувати певної заданої величини. В такому випадку достатньо знайти саме «раціональне», тобто розумне рішення. Друга немаловажна причина популярності ГА міститься в стрімкому зрості продуктивності сучасних комп’ютерів.

Переваги генетичних алгоритмів стають більш очевидними, якщо розглянути основні їх відмінності від традиційних методів. Основних відмінностей п’ять:

• 1. Генетичні алгоритми працюють з кодами, в яких представлений набір параметрів, безпосередньо залежних віх аргументів цільової функції.
• 2. Для пошуку генетичний алгоритм використовує декілька точок пошукового простору одночасно (розпаралелювання), а не переходить від точки до точки, як це робиться в традиційних методах. Тобто ГА оперує одночасно всією сукупністю припустимих рішень.
• 3. Генетичні алгоритми в процесі роботи не використовують ніякої додаткової інформації, що підвищує швидкість їх роботи.
• 4. ГА використовує як імовірнісні правила для породження нових точок пошуку, так і детерміновані правила для переходу від одних точок до інших.
• 5. Генетичні алгоритми здійснюють пошук оптимального рішення за однією й тією ж стратегією, як для унімодальних, так і для багатоекстремальних функцій.

ГА працює з кодовими послідовностями (КП) — кодами безвідносно щодо їх значеннєвої інтерпретації. Тому сама КП і її структура описуються поняттям генотип, а його інтерпретація, з боку задачі, що вирішується, поняттям фенотип. Кожна КП є, за змістом, точкою простору пошуку. Екземпляр КП називають хромосомою, істотою, індивідуумом.

В принципі, генетичні алгоритми не обмежені бінарним або цілочисельним представленням. Відомі й інші реалізації, побудовані виключно на векторах речовинних чисел. Не зважаючи на те, що для багатьох реальних задач більш підходять рядки перемінної довжини, на даний час структури фіксованої довжини є найбільш розповсюдженими й вивченими.

На кожному кроці роботи ГА використовує декілька точок пошуку одночасно. Сукупність цих точок є набором КП, які утворять вихідну множину рішень — К (популяцію). Кількість КП в популяції називають розміром популяції. На кожному кроці роботи ГА обновлює вихідну множину К шляхом створення нових КП та знищення «безперспективних», які не задовольняють критерію цільової функції. Кожне обновлення інтерпретується як зміна поколінь і звичайно ідентифікується за заданим розміром.

В процесі роботи алгоритму генерація нових КП відбувається на базі моделювання процесу розмноження. При цьому, природно, КП, що породжують, називаються батьками, а породжені КП — нащадками. Батьківська пара, як правило, породжує пару нащадків. Безпосередня генерація нових рядків з двох обраних відбувається за рахунок роботи оператора схрещування (випадково-детермінованого обміну), який в процесі роботи алгоритму може застосовуватися не до всіх пар батьків.

Частина цих пар може переходити до популяції наступного покоління безпосередньо. Те, як часто виникатиме така ситуація, залежить від імовірності застосування оператора схрещування, яка є одним із параметрів ГА. Моделювання процесу генерації нових точок пошуку відбувається за рахунок роботи оператора мутації, який задається визначеною імовірністю. Оскільки еволюційний процес біологічних видів супроводжується загибеллю останніх, то породження нащадків повинно супроводжуватися знищенням інших безперспективних КП. Вибір пар батьків з популяції для породження нащадків виконує оператор добору, а вибір КП для знищення — оператор редукції.

Характеристики генетичного алгоритму обираються таким чином, щоб забезпечити невеликий час роботи, з одного боку, та пошук як можна кращого рішення, з іншого. Загальна структурна схема генетичного алгоритму при біологічній інтерпретації зображена на рис. 7.1.

Робота генетичного алгоритму. Розглянемо роботу ГА (рис. 7.1). Формування вихідної популяції К відбувається за допомогою якогось випадкового закону, наприклад, рівномірного, на базі якого обирається необхідна кількість точок пошукового простору. Вихідна популяція може також бути результатом роботи будь-якого іншого алгоритму оптимізації.

В основі оператору добору, який служить для вибору батьківських пар та знищення КП, лежить принцип «живає найсильніший» Імовірність участі i-ї КП в процесі обміну обчислюється за формулою:

(7.1).

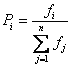
де n — розмір вихідної множини К, — номер КП, i — значення цільової функції для i-ї КП.

Оператор випадково-детермінованого обміну (схрещування) моделює природний процес спадкування, тобто забезпечує передачу властивостей новим КП (нащадкам). В теперішній час знаходять широке застосування одноточкові, двоточкові та рівномірні оператори, залежно від типу розбивки КП На рис. 7.2 представлена структура одноточкового оператору схрещування. Одноточковий оператор працює наступним чином. Спочатку, випадковим чином обирається одна з точок розриву (точка розриву — ділянка між сусідніми бітами в рядку). Обидві батьківські структури розриваються на два сегменти в цій точці. Потім відповідні сегменти різних батьків склеюються та утворюється два генотипи нащадків.

Рис. 7.1 -Загальна структура генетичного алгоритму Наприклад, припустимо, що один з батьків складається з 10 нулів, а інший — з 10 одиниць. Нехай з 9 можливих точок розриву обрана точка 3, тоді робота одноточкового оператору схрещування виглядає так, як показано на рис. 7.2.

Рис. 7.2— Структура одноточкового оператору схрещування

Йовірність застосування оператору схрещування обирається достатньо великою, у межах від 0.9 до 1. Робиться це для того, щоб забезпечити постійну появу нових КП, які розширюють простір пошуку. Слід зазначити, що для операції схрещування можуть застосовуватися також двоточкові та рівномірні оператори схрещування. В двоточковому операторі обираються дві точки розриву, та батьківські хромосоми обмінюються сегментом, який знаходиться між двома цими точками. В рівномірному операторі схрещування кожен біт першого батька спадкується першим нащадком із заданою імовірністю, у протилежному випадку цей біт передається другому нащадку. Після того, як закінчиться етап схрещування, виконуються оператори випадкової зміни КП (мутації). Оператор мутації служить для моделювання природного процесу мутації. Суть даного процесу полягає у наступному. Будь-яка популяція, якою б великою вона не була, охоплює обмежену область простору пошуку. Оператор обміну (схрещування), безумовно, розширює цю область, але все ж до певної міри, оскільки використовує обмежений набір значень, заданий вихідною множиною К (вихідною популяцією). Внесення випадкових змін до КП дозволяє перебороти це обмеження, а інколи й значно скоротити час пошуку або покращити якість результату. В процесі роботи алгоритму усі зазначені вище оператори використовується багатократно та ведуть до поступової зміни вихідної популяції. Оскільки всі оператори спрямовані на покращання кожної окремої КП, то результатом їх роботи є поступове покращання — еволюція до локально-оптимального (оптимального) рішення.

Критерієм зупинення генетичного алгоритму може бути одна з трьох подій:

• 1) сформовано задане число поколінь;
• 2) популяція досягла заданого рівня якості;
• 3) досягнуто якийсь рівень збіжності, при якому покращання популяції не відбувається.

Після роботи генетичного алгоритму з кінцевої популяції обирається та КП, яка дає мінімальне (або максимальне) значення цільової функції і є, у підсумку, результатом роботи генетичного алгоритму.

Ефективність ГА при вирішенні конкретної задачі оптимізації визначається видом генетичних операторів і вибором відповідних значень параметрів, а також способу представлення задачі на КП — хромосомі. Оптимізація цих факторів приводить до підвищення швидкості та стабільності пошуку, що є суттєвим для застосування генетичних алгоритмів.