Метод степенів. 
Алгебраїчна проблема власних значень

Цей метод застосовується для ітераційного обчислення найбільшого за модулем власного значення і відповідного власного вектора, а також власних значень, для яких відомі вже досить хороші наближення.

Нехай — матриця, яку можна звести до діагонального вигляду, з власними значеннями, для яких.

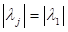
Припустимо додатково, що не існує відмінних від власних значень, для яких, тобто існує r > 0 таке, що.

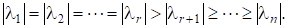
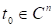
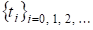
Оскільки зводиться до діагонального вигляду, то має лінійно незалежних власних векторів які утворюють базис в. Нехай — довільний вектор, а послідовність утворюється за правилом.

Вектор можна подати у вигляді.

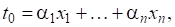
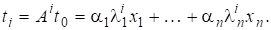
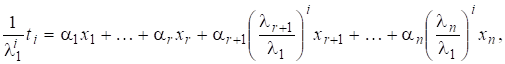
і тому в силу маємо.

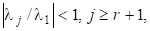
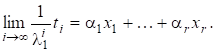
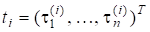
Припустимо додатково, що для має місце, тобто має «досить загальний вигляд». Нормуючи яким-небудь способом, наприклад,.

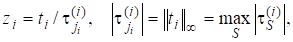
де — деяка нормуюча стала. Цей метод збігається до найбільшого за модулем власного значення і відповідного власного вектора (лінійна комбінація власних векторів, що відповідають, є також власним вектором).

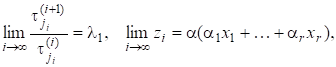
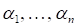
Маємо, що для (— просте власне число) граничний вектор є незалежним від вибору (якщо лише). Якщо (—многократне власне значення), то залежить від співвідношення коефіцієнтів, тобто від початкового наближення. Швидкість збіжності оцінюється величиною і є тим більшою, чим менше це число. З викладеного вище також випливає, що метод буде збігатися не до, а до і відповідного власного вектора, якщо вибрати в розвиненні для (і якщо додатково не існує відмінних від власних значень з тим самим модулем). Проте це справедливо лише теоретично, бо внаслідок неминучих похибок заокруглення ми вже після першої ітерації для дістанемо.

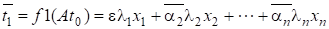
з деяким і метод, таким чином, збігатиметься до .

Якщо не зводиться до діагонального вигляду і має єдине власне значення з найбільшим модулем, то ми можемо подати через власні і головні вектори матриці А і аналогічно довести, що для досить загального вигляду метод степенів збігається до та відповідного власного вектора.

Практична обмеженість описаного вище методу полягає в тому, що він повільно збігається, якщо абсолютні значення власних чисел близькі, а також у тому, що за ним обчислюють лише одне (максимальне за модулем) власне значення і власний вектор. Цих недоліків, проте, можна позбутися за допомогою методу зворотних ітерацій, запропонованого в 1945 р. Віландтом. Цей метод застосовується тоді, коли для якогось із власних значень наприклад, відоме «досить хороше наближення», тобто.

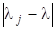
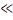
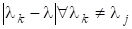
Тоді для «досить довільного» початкового вектора будується послідовність.

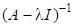
Якщо то існує і остання рівність еквівалентна.

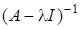
тобто цей метод є звичайним методом степенів для матриці та власних чисел, причому.

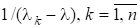
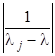
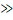
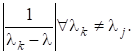
Припустивши знову, що зводиться до діагонального вигляду і має власні вектори, і поклавши дістанемо для простого.

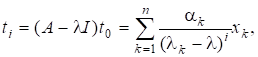
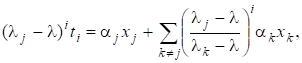
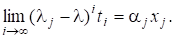
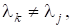
Швидкість збіжності тим більша, чим меншим є відношення для тобто чим кращим є наближення. Зауважимо, що матриця для досить хороших наближень є майже виродженою, проте можна довести, що оскільки ми шукаємо лише напрям власного вектора, то ця задача є добре обумовленою і не виникає жодних труднощів. Зазначимо також, що для обчислення досить один раз обчислитирозвинення матриці і потім з його допомогою обчислювати розв’язки систем з різними правими частинами.

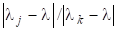
Якщо нас цікавить не найбільше за модулем власне значення або ж потрібно розв’язати повну проблему власних значень, то розглянутий вище метод для цього непридатний. Оскільки остання задача взагалі складна і багатогранна, обмежимося далі лише повною проблемою власних значень для матриць з різними власними значеннями.

Найпростіша ідея, яка здавалось би веде до розв’язування повної проблеми власних значень, полягає в тому, щоб за допомогою перетворень подібності, скажімо, за допомогою унітарних матриць, звести матрицю до діагонального вигляду. Перша ж спроба зробити це за допомогою матриць Хаусгольдера показує, що це неможливо, бо нулі, які утворюються після множення на зліва, «руйнуються» після множення на * справа:

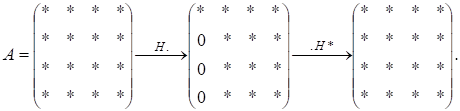
Проте легко помітити, що таким чином можна матрицю звести до так званої форми Хессенберга:

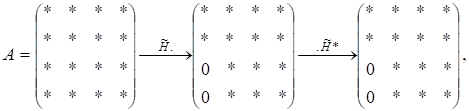
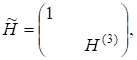
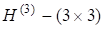
— матриця Хаусгольдера, побудована за обведеним тривимірним вектором. Якщо — ермітова матриця, то замість згаданих вище ситуацій матимемо такі:

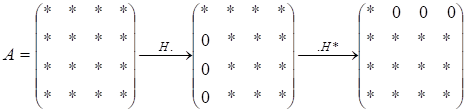
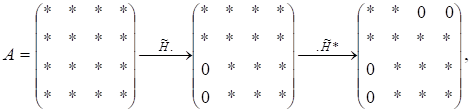
причому в силу ермітовості матриці матриця також буде ермітовою:

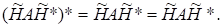
Сформулюємо ці міркування у вигляді такої леми.

Лема 2. Нехай. Тоді існує унітарна матриця Р, яка є добутком (п — 2) матриць Хаусгольдера і така, що.

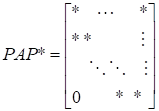
— форма Хессенберга для неермітових матриць та.

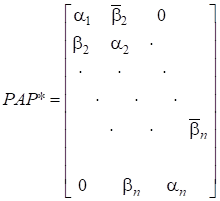
— тридіагональна ермітова матриця для ермітоеих матриць (, тобто — дійсні числа).

Д о в е д е н н я. Продовжуючи описаний вище процес за допомогою матриць відображення Хаусгольдера дістанемо.