Алгебраїчна проблема власних значень

Алгебраїчна проблема власних значень формулюється таким чином: знайти числа та вектори, для яких.

(1).

де — задана матриця з множини матриць з комплексними елементами;

— множина комплексних чисел. Числа називаються власними числами (значеннями), а відповідні вектори — правими власними векторами матриці .

Множина утворює підпростір векторів простору, і цей підпростір має розмірність Число є тоді і лише тоді власним числом матриці, коли, тобто коли >, і.

Многочлен.

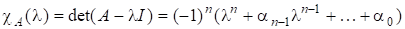
називається характеристичним многочленом матриці А, і його корені є власними значеннями А. Якщо є різними коренями, то.

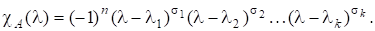
Число називається кратністю власного значення, точніше алгебраїчною кратністю.

Власні вектори матриці визначаються неоднозначно: якщо є власними векторами, що відповідають власному значенню то і є відповідним до власним вектором. Нуль-вектор разом з власними векторами якраз і заповнюють підпростір, а його розмірність, тобто максимальне число лінійно незалежних власних векторів, що відповідають, називається геометричною кратністю власного значення. Наступні приклади показують, що алгебраїчна та геометрична кратності не завжди збігаються, але можна довести, що Приклад 1. Діагональна матриця.

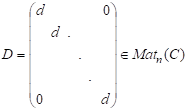
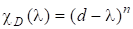
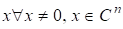
має характеристичний многочлен і є єдиним власним значенням, якому відповідає власний вектор. У даному випадку.

Приклад 2. Матриця.

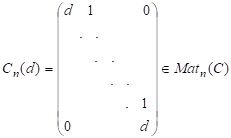
має характеристичний многочлен і є єдиним власним значенням з алгебраїчною кратністю. Але. Отже, геометрична кратність.

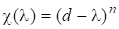
— перший координатний вектор.

В силу рівностей.

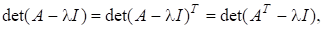
маємо: якщо є власним значенням матриці, то є власним значенням і матриці, а є власним значенням. Із співвідношень випливає, що, але між та чи та не існує таких простих співвідношень. Вектор називається спряженим до. Оскільки і, то називається ще лівим власним вектором матриці, який відповідає власному значенню. Неважко також помітити, що перетворення подібності.

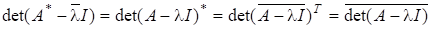
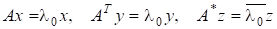
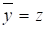
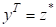
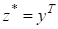
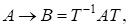
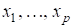
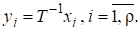
де зберігає власні значення, а відповідні власні вектори змінює за формулою. Не змінюється при цьому характеристичний поліном, а також числа та: для це випливає з інваріантності характеристичного многочлена, а для — з того, що для вектори є лінійно незалежними тоді і тільки тоді, коли лінійно незалежними є На еквівалентних перетвореннях грунтується багато чисельних методів розв’язування проблем власних значень і власних векторів.

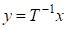
Наведемо без доведення теореми про деякі форми представлення матриць.

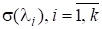
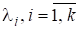
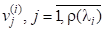
Теорема 1. Нехай, А —довільнаматриця і — її різні власні значення з геометричними та алгебраїчними кратностями. Тоді для кожного власного значення існують натуральних чисел, таких, що.

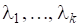
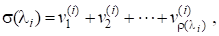
а також невироджена-матриця Т така, що матриця, яка називається нормальною формою Жордана матриці А, має вигляд.

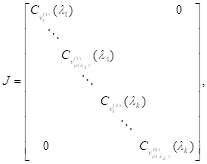
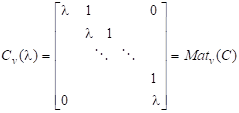
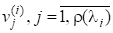
називаються жордановими клітинками. При цьому числа (а з ними і матриця J), з точністю до перестановки однозначно визначені, а матриця Т, взагалі кажучи, визначається неоднозначно.

Розщепимо матрицю за стовпчиками відповідно до нормальної форми Жордана:

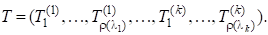
Тоді із співвідношення маємо.

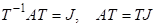
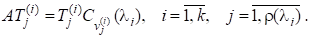
(2).

Позначимо стовпчики матриці через тобто.

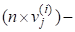
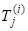
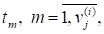
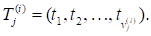
Тоді із (2) та з означення матриць дістанемо.

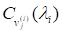
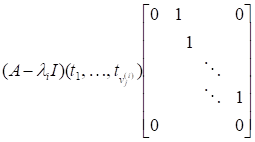
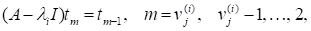
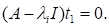
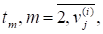
Зокрема помічаємо, що (перший стовпчик матриці) є власним вектором матриці А, що відповідає власному значенню. Інші вектори називаються головними векторами, відповідними значенню і ми бачимо, що кожній клітинці Жордана відповідає один власний вектор і набір головних векторів. В цілому для кожної матриці А можна знайти базис простору (а саме стовпчики матриці), який складається з власних та головних векторів матриці А.

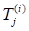
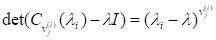
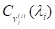
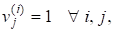
Характеристичні поліноми окремих клітинок Жордана називаються елементарними дільниками матриці А. Таким чином, матриця, А має лінійні елементарні дільники тоді і лише тоді, коли тобто жорданова нормальна форма матриці є діагональною матрицею. У цьому разі називається матрицею, що зводиться до діагонального вигляду, або матрицею, що припускає нормалізацію, тобто в є базис, який складається лише з власних векторів матриці, а головні вектори не з’являються. Отже, кожну матрицю, яка має різні власні значення, можна звести до діагнонального вигляду за допомогою перетворення подібності.

Далі розглянемо деякі класи матриць, що зводяться до діагонального вигляду. Власні вектори таких матриць утворюють базис в .

Якщо в перетворенні подібності припускати, що не довільні несингулярні матриці, то у загальному випадку не може бути зведена до форми Жордана. Для унітарних матриць Т, тобто має місце така теорема.

Теорема 2 (теорема Шура). Для довільної матриці існує унітарна матриця U така, що.

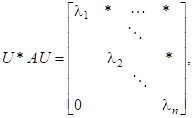
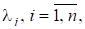
де — власні значення матриці А (не обов’язково різні).

Якщо, А = А*, тобто є ермітовою матрицею, то (U*AU)* = U*A*U** = U*AU є також ермітовою і з теореми 4 випливає така теорема.

Теорема 3. Для довільної ермітової матриці А існує унітарна матриця U така, що.

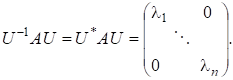
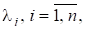
При цьому власні значення матриці А є дійсними, а і-й стовпчик матриці U є власним вектором, відповідним тобто, А має п лінійно незалежних ортогональних власних векторів.

Узагальненням ермітових є нормальні матриці, для яких А*А = АА*.

Теорема 4. Матриця є нормальною (А*А = А А*) тоді і лише тоді, коли існує унітарна матриця U така, що.

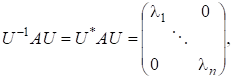
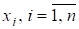
тобто нормальні матриці можна звести до діагонального вигляду, і вони мають п лінійно незалежних ортогональних векторів, які є стовпчиками матриці U.

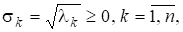
Для довільної прямокутної матриці A матриця А* А є невід'ємно визначеною з власними значеннями. Числа називаються сингулярними числами матриці А.

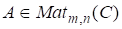
Теорема 5. Нехай. Тоді:

1) існує унітарна матриця U та унітарна матриця V такі, що матриця U*AV = є діагональною матрицею вигляду.

>

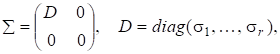
де — відмінні від нуля сингулярні числа матриці A, r — ранг матриці А;

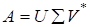
2) відмінними від нуля сингулярними числами матриці А* є також. Розвинення називається сингулярнозначним зображенням матриці А (розвинення за сингулярними значеннями).

Унітарні матриці U та V можна інтерпретувати таким чином: стовпчики матриці U являють собою m ортонормальних власних векторів ермітової матриці АА*, а стовпчики V є ортонормальними власними векторами ермітової матриці А*А, бо U*AA*U =, V*A*AV =. Діагональна матриця.

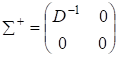
є псевдооберненою до, або оберненою матрицею Мура — Пенроуза, тобто матрицею, що задовольняє співвідношення: а; б)*; в). Тому, як легко помітити, матриця.

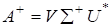
є в силу єдиності псевдооберненою до А.

Нехай власний вектор є спряженим до.

.

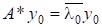
Заради простоти вважатимемо, що — просте власне значення, тобто воно є простим коренем многочлена .

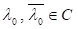
Лема 1. Нехай в простими власними значеннями матриць A,, що відповідають власним векторам та. Тоді існує неперервно диференційовне відображення деякого околу V з простору матриць з центром в, А таке, що і є простим власним значенням матриці В для всіх причому.

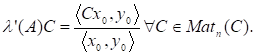
Д о в е д е н н я. Оскільки є простим власним значенням характеристичного многочлена, то.

.

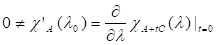
З теореми про неявну функцію випливає, що в деякому околі нуля існує неперервно диференційовне відображення таке, що і є простим власним значенням матриці. Крім того, існує неперервно диференційовна функція.

Така, що і х (t) є власним вектором матриці, який відповідає власному значенню, тобто.

Помноживши цю рівність, а також рівність скалярно на, знайдемо.

=.

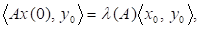
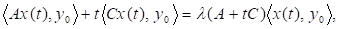
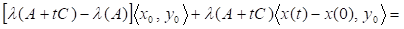
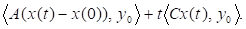
Після ділення на t і переходу до границі при дістанемо.

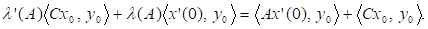
Враховуючи, що.

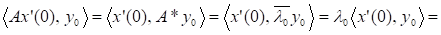
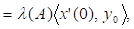
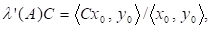
що і треба було довести.

Щоб оцінити обумовленість задачі маємо обчислити норму як лінійного відображення.

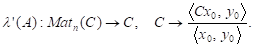
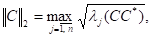
Виберемо в просторі норму, а в просторі за норму вважатимемо модуль. Тоді.

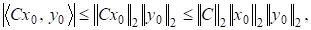
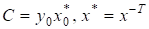
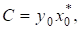
причому якщо то в першій нерівності досягається знак рівності. Це матиме місце, зокрема, для. Для матриці, очевидно, і в другій нерівності справжується знак рівності. Тому з урахуванням співвідношення маємо.

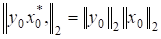
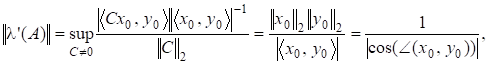
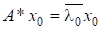
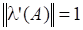
де через позначено кут між власним вектором та спряженим вектором. Для нормальних матриць, для яких за означенням, та збігаються, тобто. Тому для таких матриць .

Сформулюємо здобуті результати у вигляді теореми.

Теорема 6. Абсолютне та відносне числа обумовленості задачі обчислення простого власного значення матриці стосовно матричної норми виражаються формулами.

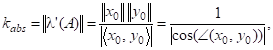
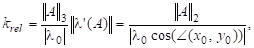
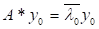
де — власний вектор матриці А, що відповідає власному значенню , — спряжений до нього власний вектор матриці *, тобто,. Зокрема, проблема власних значень для нормальних матриць є добре обумовленою з числом обумовленості .

Приклад матриці.

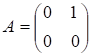
з власними значеннями та збуреної матриці.

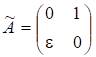
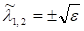
з власними значеннями показує, що для несиметричних матриць проблема власних значень може бути, взагалі кажучи, погано обумовленою. Дійсно,.

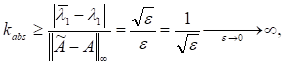
тобто задача обчислення власного значення матриці стосовно абсолютної похибки взагалі не є коректно поставленою задачею. Інший приклад, розглянутий у вступі (п. 2), показує, що обчислення власних значень як коренів характеристичного многочлена (навіть добре розділених і однократних) хоча теоретично і можливе, але потребує великої обережності. Тому на практиці, як правило, застосовуються інші методи, деякі з яких ми розглянемо далі.