Параметри геометричних фігур у просторі.
Параметри точки

Дві функціональні залежності між параметрами точки вилучають з простору однопараметричну множину точок, що в загальному випадку належать просторовій кривій лінії. Наприклад, при зв’язуванні параметрів системою рівнянь (1.2) і (1.3) з простору вилучається просторова крива четвертого порядку, яка є результатом перетину сфери (1.2) з параболічним циліндром (1.3). Якщо одна з двох залежностей… Читати ще >
Параметри геометричних фігур у просторі. Параметри точки (реферат, курсова, диплом, контрольна)
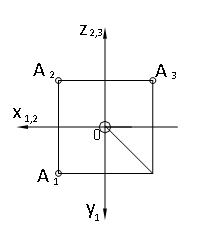
Точка у просторі визначається трьома параметрами, які зокрема можуть бути координатами у різних координатних системах. У прямокутній декартовій координатній системі (рис. 1.1) за параметри точки приймають її абсцису, ординату і аплікату. При звільненні трьох параметрів точки простір заповнюється трипараметричною множиною точок () і тому називається тривимірним точковим простором.
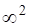
Рис. 1.1. Параметри точки.
При зв’язуванні одного параметра функціональною залежністю (1.1).
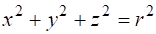
з простору вилучається двопараметрична множина точок, яка у загальному випадку визначає поверхню, або площину. Наприклад, залежність.
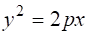
(1.2).
вилучає з простору двопараметричну множину точок, що належать сфері (рис. 1.1), а залежність.
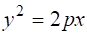
(1.3).
утворює поверхню горизонтально-проеціювального параболічного циліндра (рис. 1.2).
Рис. 1.2. Проекціювальна площина.
При нелінійній функції (1.1) у просторі утворюється поверхня. Якщо функція (1.1) лінійна — утворюється площина. Якщо функція (1.1) містить тільки два параметри, то утворюється проекціювальний циліндр (рис. 1.3) або проекціювальна площина. Якщо функція (1.1) містить лише один параметр, наприклад,, то утворюється площина рівня.
Дві функціональні залежності між параметрами точки вилучають з простору однопараметричну множину точок, що в загальному випадку належать просторовій кривій лінії. Наприклад, при зв’язуванні параметрів системою рівнянь (1.2) і (1.3) з простору вилучається просторова крива четвертого порядку, яка є результатом перетину сфери (1.2) з параболічним циліндром (1.3). Якщо одна з двох залежностей — лінійна, утворюється плоска крива. При двох лінійних залежностях (1.1) вилучається однопараметрична множина точок, що належить прямій лінії. Дві залежності між параметрами завжди можна привести до двох рівнянь, які описують дві проекції лінії, що вилучаються з точкового простору.