Розділ 3. Симплексний метод як метод отримання розв'язку прямої та двоїстої задач

Де — лінійно незалежні вектори і план є кутовою точкою багатогранника розв’язків, а отже, може бути початковим опорним планом. Так як вже відомим є опорний план, можна будувати першу симплекс таблицю. Якщо існує кілька однакових значень оцінок, що відповідають, то з відповідних їм векторів до базису включають той, якому відповідає максимальне значення функціонала. Тобто мінімальне значення… Читати ще >
Розділ 3. Симплексний метод як метод отримання розв'язку прямої та двоїстої задач (реферат, курсова, диплом, контрольна)
Початковий опорний план
Розглянемо задачу лінійного програмування, записану в канонічній формі:
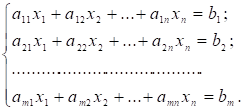
.
Не порушуючи загальності, допустимо, що система рівнянь містить перші m одиничних векторів. Отримаємо:
(3.1).
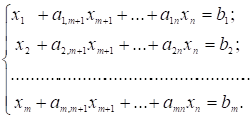
(3.2).
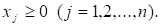
(3.3).
Система обмежень (3.2) у векторній формі матиме вигляд:
(3.4).
Де.
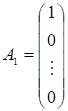
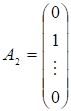
,…, ,.
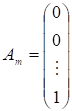

…,, ,.
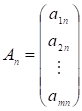
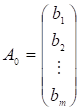
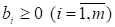
— лінійно незалежні одиничні вектори m-вимірного простору, що утворюють одиничну матрицю і становлять базис цього простору. Тому в розкладі (3.4) базисними змінними будуть, а інші змінні — вільні. Прирівняємо всі вільні змінні до нуля, тобто. Оскільки, а вектори — одиничні, то отримаємо один із розв’язків системи обмежень (3.2):
(3.5).
тобто допустимий план.
Такому плану відповідає розклад.
(3.6).
де — лінійно незалежні вектори і план є кутовою точкою багатогранника розв’язків, а отже, може бути початковим опорним планом. Так як вже відомим є опорний план, можна будувати першу симплекс таблицю.
Перевірка плану на оптимальність за допомогою оцінок
Після заповнення симплексної таблиці розраховують значення оцінок плану:
.
Потім згідно з умовою оптимальності плану задачі лінійного програмування, якщо всі.
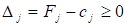
(для задачі на максимум), то план є оптимальним. Допустимо, що одна з оцінок.
.
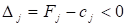
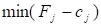
тоді план не є оптимальним і необхідно здійснити перехід до наступного опорного плану, якому буде відповідати більше значення функціонала. Якщо від'ємних оцінок кілька, то включенню до базису підлягає вектор, який вибирається як. Мінімум знаходять для тих індексів j, де.
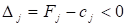
.
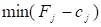
Якщо існує кілька однакових значень оцінок, що відповідають, то з відповідних їм векторів до базису включають той, якому відповідає максимальне значення функціонала.
Якщо хоча б для однієї від'ємної оцінки.
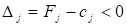
всі коефіцієнти розкладу відповідного вектора недодатні, то це означає, що функціонал є необмеженим на багатограннику розв’язків, тобто багатогранник у даному разі являє собою необмежену область і розв’язком задачі є .
Нехай.
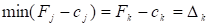
.
тобто мінімальне значення досягається для k-го вектора. Тоді до базису включається вектор. Відповідний стовпчик симплексної таблиці називають розв’язковим.
Для того, щоб вибрати вектор, який необхідно вивести з базису, розраховують останній стовпчик — значення :
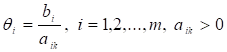
.
З розрахованих значень необхідно вибрати найменше. Тоді з базису виключають i-ий вектор, якому відповідає .
Допустимо, що.
відповідає вектору, що знаходиться в l-му рядку. Відповідний рядок симплексної таблиці називають розв’язковим.
Перетином напрямного стовпчика та напрямного рядка визначається елемент симплексної таблиці alk, який називають розв’язковим елементом. За допомогою елемента alk і методу Жордана—Гаусса розраховують нову симплексну таблицю, що визначатиме наступний опорний план задачі.