Параметри форми і положення геометричних фігур у просторі

Число параметрів, що визначають єдину фігуру у просторі, називається її параметричним числом. При певних обставинах всі параметри фігури можна розділити на параметри форми фігури і параметри положення. Положення будь-якої фігури у просторі в загальному випадку визначається шістьма параметрами, які відповідають шести степеням вільності фігури у просторі. Будь-яке складне переміщення у просторі можна уявити як ланцюг послідовних елементарних переміщень: три прямолінійно-поступальних переміщення уздовж координатних осей, або уздовж довільних непаралельних прямих, що не належать одній площині, і три обертання навколо координатних осей, або навколо трьох довільних непаралельних осей, що не належать одній площині (рис. 1.7). Кожне з цих елементарних переміщень задається одним параметром. Тому число параметрів положення фігури дорівнює шести. З цього правила є винятки, якщо існують рухи, які не переводять фігуру в інше положення. Наприклад, пряма лінія не змінює свого положення у просторі при обертанні навколо себе, як навколо осі. Пряма (нескінченна) також не змінює свого положення при поступальному переміщенні уздовж самої себе. Тому пряма у просторі має на два переміщення менше, ніж довільна фігура, а саме — чотири. Число параметрів положення зменшується для всіх фігур обертання (поверхні обертання, коло) для всіх гвинтових фігур (циліндрична гвинтова лінія, гвинтові поверхні), для точки і площини. Число параметрів форми фігури залежить від складності її форми і для різних фігур може бути різним. Число параметрів форми фігури відповідає числу її розмірів, за якими визначається єдина фігура, незалежно від її положення у просторі.

Рис. 1.7. Положення геометричних фігур у просторі.

Приклад 1. Визначити число параметрів форми і положення довільної трикутної піраміди (рис. 1.8).

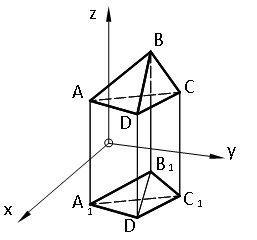
Рис. 1.8. Піраміда у просторі.

Єдина трикутна піраміда визначається чотирма вершинами, кожна з яких задається трьома параметрами. Тому параметричне число такої піраміди:

.

Шість з цих параметрів є параметрами положення, решта — параметри форми:

.

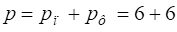
Дійсно, піраміду певної форми можна задати, якщо задати довжини шести її ребер.

Приклад 2. Визначити число параметрів форми і положення довільно розміщеної у просторі сфери. (рис. 1.24). Форма сфери визначається одним параметром — радіусом або діаметром. Число параметрів положення дорівнює:

.

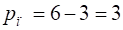
оскільки існують обертання навколо трьох осей сфери, що не переводять її в інше положення.

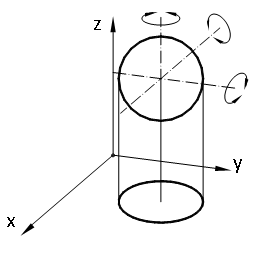
Рис. 1.8. Сфера у просторі.

Отже, сфера має три параметри положення і один параметр форми:

.

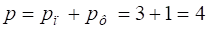
Параметричне число геометричної фігури можна визначити і за її аналітичним описом. Так, наприклад, трикутну піраміду (рис. 1.23) можна отримати як результат перетину чотирьох площин, кожна з яких визначається трьома параметрами, які присутні у рівнянні площини у вигляді коефіцієнтів ():

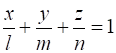
.(1.4).

Отже чотири площини, кожна з яких визначається трьома параметрами, разом дають 12 параметрів трикутної піраміди, але у цьому випадку не можна відокремити параметри форми від параметрів положення.

Просторова крива, яка задана системою рівнянь своїх проекцій:

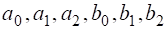
має шість параметрів:.

Поверхня другого порядку:

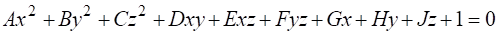
(1.6).

має дев’ять параметрів за числом незалежних коефіцієнтів у рівнянні, але ці коефіцієнти не можна кваліфікувати як параметри форми і положення поверхні, оскільки вони є функціями від відповідних параметрів.

Геометричну фігуру можна розмістити відносно координатних осей таким чином, що параметри положення дорівнюватимуть нулю. Тоді в аналітичному описі фігури будуть присутніми тільки параметри форми. Зокрема рівняння поверхні, у якому відсутні параметри її положення називається канонічним. Наприклад, канонічне рівняння тривісного еліпсоїда:

(1.7).

де — довжини півосей еліпсоїда (параметри форми) [3, 4, 5].