Вступ.
Визначення мінімального шляху на графі з ребрами довільної довжини

Задати граф означає задати множини його вершин та ребер, а також відношення інцидентності. Крім графічного, є інші способи задання графа. Якщо граф скінчений, для опису його вершин та ребер достатньо їх занумерувати. Нехай v1, v2, … vn — вершини графа, e1, e2, … em — його ребра. Відношення інцидентності можна визначити матрицею, що має m рядків та n стовпчиків і складається з елементів еij… Читати ще >
Вступ. Визначення мінімального шляху на графі з ребрами довільної довжини (реферат, курсова, диплом, контрольна)
Є багато підходів до визначення поняття «граф». Наведемо одне з таких визначень. Нехай V — довільна множина, E — деяка сукупність пар вигляду (vi, vj), де vi, vj V (тобто сукупність пар елементів, що входять до множини V), причому в сукупності E можуть зустрічатися однакові пари. Тоді упорядкована пара G=(V, E), що складається з множини V та сукупності E, називається графом із множиною вершин V та множиною ребер E. Іншими словами, граф — це дві множини, що взаємно відповідають одна інший, — множина вершин та множина ребер (множина бінарних відношень вершин), кожне (ребро) з яких відповідає парі елементів (допускаються однакові елементи) з множини вершин.
Графи зручно зображати графічно (малюнком), що спричинило появу їхньої назви. При цьому елементи множини вершин V зображають крапками на площині, а ребра (vi, vj) — відрізками (прямолінійними або криволінійними), які з'єднують крапки vi та vj. Граф називається скінченним, якщо множини його вершин та ребер є скінченими (надалі розглядаються лише такі графи). Множину вершин графа G позначають V (G), а множину ребер — E (G). Кількість вершин графа n (G)=|V (G)| (кількість елементів V (G)). Кількість ребер графа m (G)=|E (G)| (кількість елементів E (G)). Кількість вершин графа називають його порядком.
Якщо елемент e (ребро) сукупності E є парою елементів (вершин) v та w: e=(v, w), то кажуть:
- — вершини v та w суміжні;
- — вершини v та w є кінцями ребра e;
- — вершини v та w — інцидентні ребру e;
- — ребро e — інцидентне вершинам v та w.
Іншими словами, якщо вершини є кінцями ребра, то вони інцидентні цьому ребру, а ребро — інцидентне їм. Два ребра називають суміжними, якщо обидва вони є інцидентними одній вершині (тобто мають спільну вершину). Кількість ребер, інцидентних деякій вершині v, називається локальним степенем або просто степенем вершини v.
Графічне представлення деяких прикладів графів наведено на рис. 1.
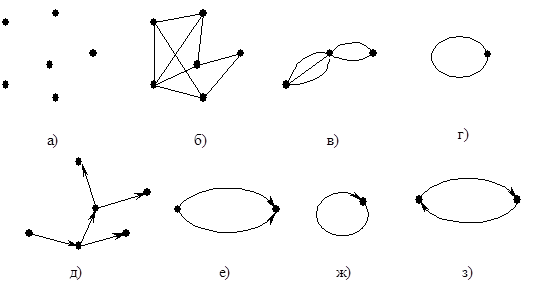
Рис. 1.
Якщо множина ребер E порожня (рис. 1, а), граф називається нуль-графом. Якщо множина вершин V є порожньою, то порожньою є також множина ребер E. Такий граф називається порожнім. Лінії, що зображають ребра графа, можуть перетинатися, але точки перетину не є вершинами (рис. 1, б). Різні ребра можуть бути інцидентні одній і тій самій парі вершин (рис. 1, в), такі ребра називаються кратними (випадок наявності однакових пар (vi, vj)). Граф, що містить кратні ребра, називається мультиграфом. Ребро може з'єднувати вершину саму з собою (рис. 1, г), таке ребро називається петлею. Це випадок наявності пар (vi, vi). Граф із петлями та кратними ребрами називається псевдографом.
Якщо пара e=(v, w) E вважається впорядкованою, тобто суттєвим є порядок розташування кінців ребра (іншими словами, важливим є, яка вершина ребра є початком, а яка — кінцем), то таке ребро називається орієнтованим. В такому випадку (w, v)?(v, w). Граф, що містить лише орієнтовані ребра, називається орієнтованим.
Якщо немає різниці, яку вершину ребра вважати початком, а яку — кінцем, тобто (w, v)=(v, w), ребро є неорієнтованим. Граф, що містить тільки неорієнтовані ребра — неорієнтований. Іноді граф може містити як орієнтовані, так і неорієнтовані ребра (змішаний граф). Ребра орієнтованого графа прийнято називати дугами і позначати направленими відрізками (рис. 1, д-з). Напрямки орієнтованих ребер позначаються стрілками. Орієнтований граф може мати кратні ребра (рис. 1, е), петлі (рис. 1, ж), а також петлі, що з'єднують одні й ті самі вершини, але у зворотних напрямках (рис. 1, з). Кожному неорієнтованому графу можна поставити у відповідність орієнтований граф з тією самою множиною вершин та множиною ребер, в якій кожне ребро замінено двома орієнтованими ребрами, що є інцидентними тим самим вершинам та мають зворотні напрямки. Про дугу (w, v) кажуть, що вона виходить з вершини w та приходить в вершину v. Вершини w та v називають відповідно початком та кінцем дуги (w, v).
Задати граф означає задати множини його вершин та ребер, а також відношення інцидентності. Крім графічного, є інші способи задання графа. Якщо граф скінчений, для опису його вершин та ребер достатньо їх занумерувати. Нехай v1, v2, … vn — вершини графа, e1, e2, … em — його ребра. Відношення інцидентності можна визначити матрицею, що має m рядків та n стовпчиків і складається з елементів еij. Стовбці відповідають вершинам графа, а рядки — його ребрам. Якщо ребро ei є інцидентним вершині vj, тоді елемент еij = 1, інакше еij = 0. Така матриця називається матрицею інцидентності звичайного графа і є одним зі способів його визначення. Для графа на рис. 2 — матриця інцидентності наведена в табл.1.
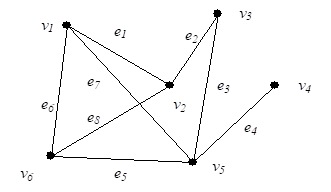
Рис. 2.
Для орієнтованого графа прийнято, що елемент еij = -1, якщо вершина vj є початком ребра ei; еij = 1, якщо вершина vj є кінцем ребра ei; еij = б (-1, 0, 1), якщо ei — петля інцидентної вершини vj; інакше еij = 0.
Граф можна задати матрицею суміжності - квадратною матрицею дij, стовпцям і рядкам якої відповідають вершини графа. Для неорієнтованого графа дij дорівнює кількості ребер, інцидентних i-тій та j-тій вершинам (кількості ребер, що їх з'єднують), для орієнтованого графа цей елемент відповідає кількості ребер з початком в i-тій вершині та кінцем в j-тій вершині. Таким чином матриця суміжності неорієнтованого графа є симетричною (дij = дji), а орієнтованого — необов’язково. Якщо ж вона є все-таки симетричною, то для кожної дуги орієнтованого графа існує дуга, що з'єднує ті ж вершини, але в зворотному напрямку.
Матриця суміжності для графа на рис. 2 наведена в таблиці 2.
Таблиця 1. Матриця інцидентності.
Содержание: {p}v1 | v2 | v3 | v4 | v5 | v6 | |
e1 | ||||||
e2 | ||||||
e3 | ||||||
e4 | ||||||
e5 | ||||||
e6 | ||||||
e7 | ||||||
e8 |
Таблиця 2. Матриця суміжності.
v1 | v2 | v3 | v4 | v5 | v6 | |
v1 | ||||||
v2 | ||||||
v3 | ||||||
v4 | ||||||
v5 | ||||||
v6 |
Маршрутом (шляхом) у графі називається така скінченна або нескінченна послідовність вершин і ребер, що чергуються: (… v1, e1, v2, e2, …, vn-1, en-1, vn, …), що кожні два сусідні ребра ei-1 та ei мають спільну інцидентну вершину vi. В скінченних маршрутах існує перше та останнє ребра, а також перша (початок маршруту) та остання (кінець маршруту) вершини.
Граф називається зваженим, якщо на множині ребер визначено вагову функцію (кожному ребру поставлена у відповідність вага). Для будь-якого шляху М зваженого графу позначимо через l (M) суму ваг ребер, що входять у М. Величину l (M) будемо називати вагою (або довжиною) шляху М у зваженому графі. Шлях у зваженому графі з вершини w в вершину v, де w v, називається мінімальним, якщо він має найменшу вагу серед усіх шляхів з вершини w в вершину v.
Існує багато практичних задач, що зводяться до пошуку мінімального шляху на графах (задачі мінімізації транспортних, енергетичних, інформаційних тощо потоків, пошуку оптимальних послідовностей виконуваних дій, наприклад оптимальної послідовності запуску партій виробів тощо).
Розглянемо алгоритм знаходження оптимального за мінімумом довжини (найкоротшого) шляху в неорієнтованому графі з ребрами довільної довжини (ваги). Нехай задано граф, у якого відомо ваги всіх ребер та вершини якого пронумеровано за порядком. Також задано початкову та кінцеву вершини шляху (яка точка є початком, а яка є кінцем, значення не має). Позначимо початок шляху — А, кінець — В. Нехай вага ребра, що з'єднує i-ту та j-ту вершини, буде позначатися Lij. Алгоритм передбачає присвоєння кожній вершині певного індексу (аналог потенціалу в електричних схемах) та має два етапи — етап визначення індексів всіх вершин та етап прокладання шляху по ребрам, вага яких рівна різниці індексів інцидентних вершин (вершин, які з'єднуються даним ребром). Отже,.