Множинна кореляція. 
Статистичне вивчення виробництва картоплі

На практиці економічного аналізу часто доводиться вивчати явища, які складаються під впливом не одного, а багатьох різних факторів, кожний з яких окремо може не справляти вирішального впливу. Спільний же вплив може бути досить сильним. Методи вимірювання кореляційного зв’язку одночасно між двома чи більше ознаками становлять вчення про множинну кореляцію. Множинна кореляція дає змогу оцінити зв’язок результативної ознаки з будь-якою факторною при фіксованому значенні інших, включених в регресійну моделі.

При теоретичному обґрунтуванні моделі і виборі факторних ознак слід враховувати тісноту кореляційного зв’язку між ознаками. При наявності зв’язку, який близький до функціонального (мультиколінеарності), оцінки параметрів багатофакторного рівняння регресії будуть ненадійними. Для оцінки мультиколінеарності між ознаками достатньо обчислити відповідні коефіцієнти кореляції. Якщо коефіцієнт кореляції двох факторних ознак близький до одиниці, то одну з них треба виключити. На цьому етапі важливо не тільки вибрати фактори, але й розкрити структуру взаємозв'язку між ними.

Складною є проблема обґрунтування функціонального виду багатофакторного рівняння регресії. Аналіз парних зв’язків непридатний, тому що фактори взаємозв'язані, а визначити зв’язок між і при фіксованих значеннях інших факторних ознак дуже складно. Тому на практиці найчастіше використовують багатофакторні лінійні рівняння і рівняння, що приводяться до лінійного виду відповідними перетвореннями, тобто:

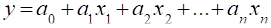
Параметр рівняння a₁ називають частинним коефіцієнтом регресії. Він показує, як у середньому змінюється результативна ознака у зі зміною факторної ознаки x_i на одиницю за умови, що інші факторні ознаки залишаються незмінними.

Для визначення параметрів треба скласти і розв’язати систему нормальних рівнянь.

Для оцінки тісноти зв’язку при множинній кореляції використовують парні та часткові коефіцієнти кореляції, множинний коефіцієнт кореляції та детермінації, а також часткові коефіцієнти детермінації.

А) Парні коефіцієнти кореляції (характеризують тісноту зв’язку між двома ознаками без врахування дії інших ознак):

; ;

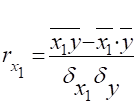
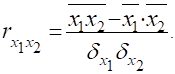
Б) часткові коефіцієнти.

Визначення зв’язку в моделях множинної регресії доповнюється оцінкою тісноти зв’язку з кожною факторною ознакою окремо. Для цього застосовують часткові коефіцієнти. Вони характеризують тісноту зв’язку результативної ознаки з однією факторною ознакою, при умові, що інші факторні ознаки перебувають на постійному рівні:

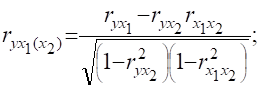
В) Множинний коефіцієнт кореляції(характеризує тісноту зв’язку між всіма досліджуваними у моделі ознаками):

.

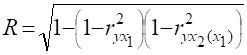
Чим більш прямолінійною є залежність, тим більш множинний коефіцієнт кореляції відповідає індексу кореляції.

Г) Множинний коефіцієнт детермінації (за його допомогою визначають тісноту зв’язку між результативною ознакою і сукупністю факторних ознак):

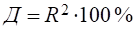
Д) часткові коефіцієнти детермінації.

У свою чергу множинний коефіцієнт детермінації розкладають на часткові коефіцієнти детермінації, які характеризують на скільки відсотків варіація результативної ознаки залежить від варіації кожної з факторних ознак.

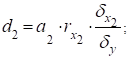
У множинній кореляції обчислюють також коефіцієнт еластичності та ?- коефіцієнт.

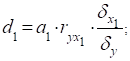
Коефіцієнт еластичності (показує на скільки процентів зміниться результативний показник при зміні факторного на 1%).

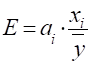
?- коефіцієнт (показує на скільки квадратичних відхилень змінюється результативний показник при зміні факторної ознаки на 1 середнє квадратичне відхилення).

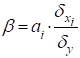
Перевірку істотності зв’язку здійснюють за допомогою F-критерію та коефіцієнтів детермінації.

:

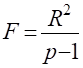
Перевірка суттєвості регресії здійснюють за формулою:

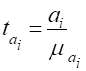
де.

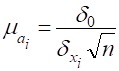
— характеризує вплив факторів, які не досліджуються в моделі і обчислюється:

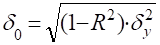
Розрахункова частина.

Побудувати рівняння регресії, що описує залежність результативної ознаки від двох факторних ознак). Перевірити суттєвість коефіцієнтів регресії а₁ і а₂. Перевірити суттєвість множинних коефіцієнтів кореляції.

Таблиця 3.2.

№ п/п.	Урожайність картоплі, ц/га.	внесено орг. добрив.	витрати праці.	Розрахункові дані.
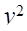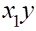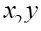			3,3.			10,89.		508,2.
			2,9.			8,41.		597,4.	34,8.
			1,8.			3,24.		131,4.	46,8.
			1,9.			3,61.		174,8.	32,3.
			2,8.			7,84.		632,8.	30,8.
			3,2.			10,24.			38,4.
			1,9.			3,61.			36,1.
			2,1.			4,41.		388,5.
			2,5.			6,25.			42,5.
			2,8.			7,84.		467,6.
			2,3.			5,29.		234,6.	36,8.
			2,5.			6,25.
			3,1.			9,61.		263,5.	52,7.
			2,9.			8,41.		188,5.	40,6.
			2,8.			7,84.		355,6.	39,2.
			3,3.			10,89.		237,6.
			3,2.			10,24.			35,2.
			1,7.			2,89.			47,6.
			2,5.			6,25.			37,5.
			1,9.			3,61.		484,5.	53,2.
			1,6.			2,56.			43,2.
			2,1.			4,41.		285,6.	29,4.
			62,1.			161,59.		9271,6.	1002,1.

Складаємо систему нормальних рівнянь:

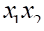
Таблиця 3.3.

Отже.

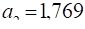
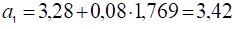
Отже рівняння регресії матиме вигляд:

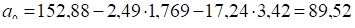
Показник показує, що зростання внесених добрив на 1 т/га призводить до збільшення врожаю картоплі на 3,42 ц/га, показник показує, що зростання витрат праці на 1 люд/год на 1 ц веде до зростання врожайності картоплі на 1,769 ц/га, при умові, що інші фактори не включені в модель залишаються на постійному рівні.

Оцінка тісноти зв’язку.

1. Парні коефіцієнти кореляції.

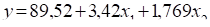
. Зв’язок прямий, тісний.

Зв’язок обернений помірний.

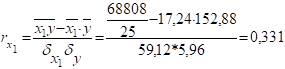
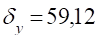
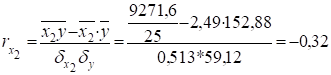
зв’язок обернений.

2. Часткові коефіцієнти кореляції.

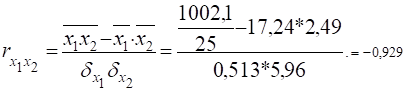
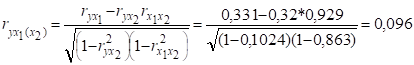
1. Множинний коефіцієнт кореляції.

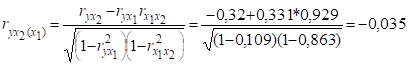
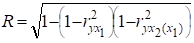
2. Множинний коефіцієнт детермінації.

3. Часткові коефіцієнти детермінації.

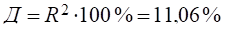
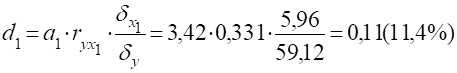
4. Коефіцієнти еластичності.

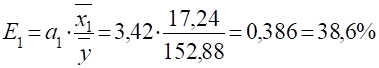
Оцінка суттєвості коефіцієнтів регресії.

Здійснюється за допомогою tкритерія, фактичне значення якого обчислюється за формулою:

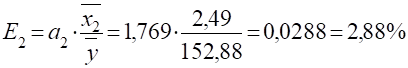
де.

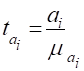
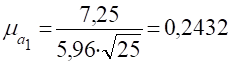
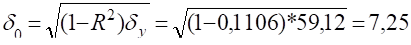
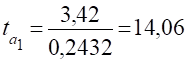
Визначаємо критичну точку: Р=0,95 V=25−2=23.

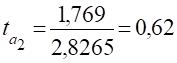
тому гіпотеза відхиляється і коефіцієнти регресії є суттєвими.

Суттєвість множинних коефіцієнтів кореляції.

Перевіряємо за Fкритерієм Фішера:

:

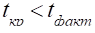
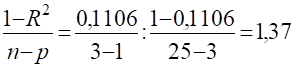
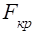
тому множинні коефіцієнти кореляції є несуттєвими.