QR-метод.
Алгебраїчна проблема власних значень

Вказаний вище недолік б) -алгоритму, а саме повільна збіжність при можна усунути за допомогою так званої стратегії зсувів (Shift-strategy). Для цього на кожному ітераційному кроці і застосовується параметр зсуву і послідовність визначається таким чином: (-розвинення), Неважко довести, що для тридіагональних симетричних матриць (див. леми 3, 4). Цей алгоритм потребує ~ множень для перетворення… Читати ще >
QR-метод. Алгебраїчна проблема власних значень (реферат, курсова, диплом, контрольна)
На ідеї зведення матриці до «простішого» вигляду за допомогою перетворень подібності будується ряд чисельних методів. Проте розглянемо спочатку загальнішийметод, який ефективно використовується на практиці. Історично цей метод, запропонований Ф. Френсісом у 1959 р. і В. М. Кублановською в 1961 p., можна розглядати як розвиненняметоду Рутісхаузера (1958 p.). Алгоритмічно вони дуже схожі, лише в останньому — замістьрозвинення матриць застосовуєтьсярозвинення, що є недоліком, борозвинення існує не для всіх матриць (навіть невироджених). -poзвинення матриці існує завжди, але з точністю до так званої фазової матриці.
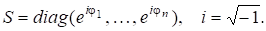
Дійсно, якщо, А = QR, де Q — унітарна матриця (), то разом з Q є унітарною матриця QS і .
Сутьалгоритму полягає в побудові послідовності матриць за правилом: (-розвинення), Ми бачили, щорозвинення матриць можна виконати, наприклад, за допомогою чисельно стійких перетворень Хаусгольдера.
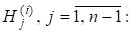
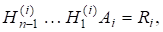
де є верхньою трикутною матрицею. Оскільки для перетворень Хаусгольдера маємо, то.
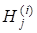
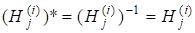
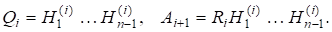
Лема 3. Матриці а також матриці.
мають такі властивості:
1) є подібною до тобто.
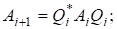
- 2)
- 3)
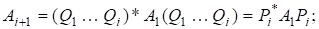
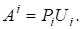
Д о в е д е н н я. 1) Оскільки, то.
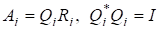
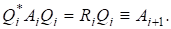
- 2) Це твердження є елементарним наслідком 1).
- 3) Із властивості 2) випливає, що
Наступна теорема, доведення якої проведемо за Вілкінсоном, доводить збіжністьалгоритму.
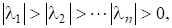
Теорема 7. Нехай матриця має такі власні значення, що (3).
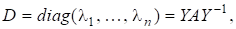
і нормальну жорданову форму в якій матриця Y має LR-розвинення.
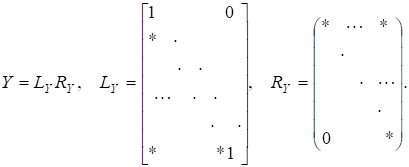
Тоді матриці визначені в QR-алгоритмі, мають такі властивості збіжності: існують фазові матриці.
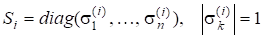
- 1)
- 2)
де — елементи матриці.
Д о в е д е н н я. Оскільки і існує, то.
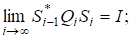
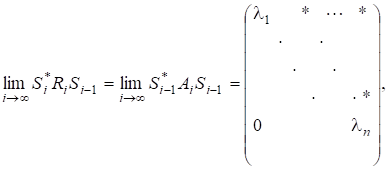
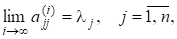
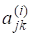
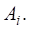
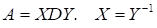
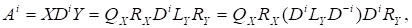
(4).
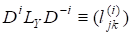
де єрозвиненням невиродженої матриці в добуток унітарної матриці та невиродженої верхньої трикутної матриці. Неважко помітити, що матриця є нижньою трикутною матрицею, причому.
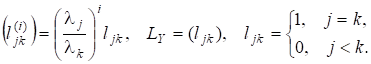
Оскільки для, то для, а також.
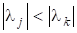
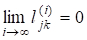
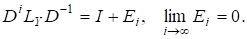
Тому із (11) маємо.
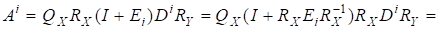
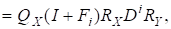
(5).
де.
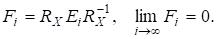
Розглянемо далі додатно визначену матрицю.
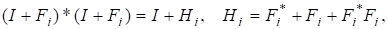
в якій і скористаємося тим фактом, що будь-яка додатно визначена матриця має розвинення.
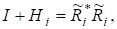
де є верхньою трикутною матрицею з додатними діагональними елементами. При цьому зазначимо, що множник залежить неперервно від матриці, тому.
Матриця.
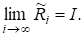
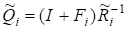
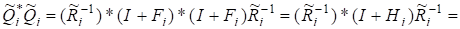
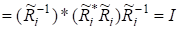
Це означає, що матриця маєрозвинення.
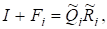
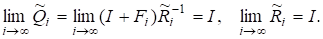
Тому з (12) маємо.
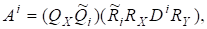
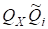
де матриця є унітарною, а матриця — верхньою трикутною. З іншого боку, з леми 4 випливає; що матриця має такожрозвинення.
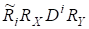
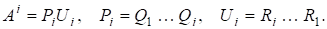
Оскількирозвинення матриць єдине з точністю до деякої фазової матриці, то існують матриці.
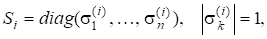
і оскільки, то.
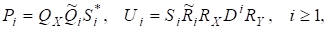
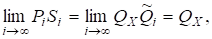
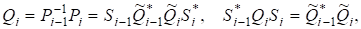
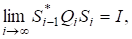
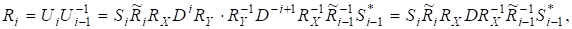
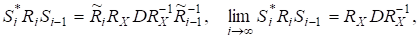
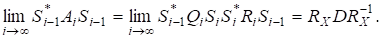
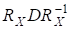
Матриця є верхньою трикутною вигляду.
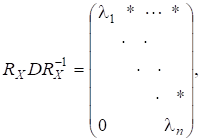
Збіжністьалгоритму можна довести і при слабкіших обмеженнях, ніж в теоремі 9. Якщо, наприклад,.
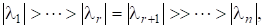
(6).
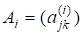
то для матриць можна довести таку теорему.
Теорема 8. Нехай із умов теореми 7 замість (3) виконується (6). Тоді.
а).
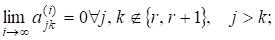
б).
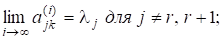
в) хоча матриці.
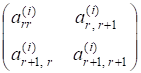
при не збігаються, а їхні власні значення збігаються до та тобто.

де збіжність має місце для елементів, які позначені та, а також для власних значеньматриць, позначених, які збігаються до та .
Можна також довести, що коли матриця зводиться до діагонального вигляду.
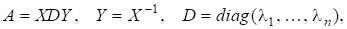
але Y не маерозвинення, тометод все одно збігається, лише в граничній матриці діагональні елементи, які є власними значеннями матриці, не обов’язково будуть впорядкованими за значеннями модуля.
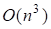
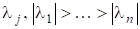
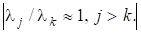
Звернемо увагу на такі недолікиалгоритму в описаній вище формі: а) якщо матриця повністю заповнена, то на кожному кроці потрібно виконати операцій; б) збіжність алгоритму невисока, якщо власні значення погано розділені, тобто .
Щоб усунути перший недолік, тобто зменшити кількість арифметичних операцій, матрицю за допомогою перетворень подібності зводять спочатку до форми Хессенберга (для матриць загального вигляду):
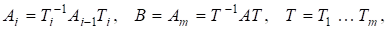

або до тридіагонального вигляду (для ермітових, зокрема симетричних, матриць):
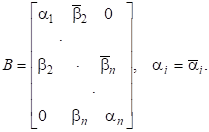
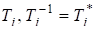
Це можна зробити, використовуючи лише унітарні матриці. Доведемо лему для симетричних матриць з дійсними компонентами, якщо — послідовність матриць залгоритму, тобто .
Лема 4. Матриці мають такі властивості:
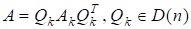
- 1) подібні до, тобто ;
- 2) якщо є симетричною, то симетричними є і матриці ;
- 3) якщо є симетричною тридіагональною матрицею, то такими самими є і, якщо реалізуються за допомогою поворотів Гівенса.
Д о в е д е н н я. 1) Це твердження доведене в лемі 3.
2) Це твердження є наслідком властивості 1) і того, що для.
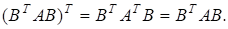
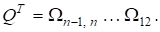
3) Нехай є симетричною тридіагональною матрицею. Реалізуємо за допомогою поворотів Гівенса так, що Позначаючи через елементи, які виключаються, а через нові ненульові елементи, дістаємо:


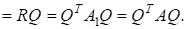
За властивістю 2) матриця має бути знову симетричною, тому всі елементи, які позначені, в насправді дорівнюють нулю. Отшже, є тридіагональною.
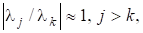
Вказаний вище недолік б) -алгоритму, а саме повільна збіжність при можна усунути за допомогою так званої стратегії зсувів (Shift-strategy). Для цього на кожному ітераційному кроці і застосовується параметр зсуву і послідовність визначається таким чином: (-розвинення), Неважко довести, що для тридіагональних симетричних матриць (див. леми 3, 4).
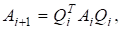
Послідовність збігається до зі швидкістю.
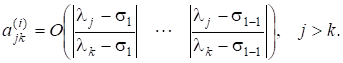
Параметри мають лежати якомога ближче до. Вілкінсон запропонував такий метод вибору параметрів зсуву для симетричної тридіагональної матриці: якщо.
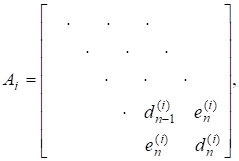
то за вибирається те власне значенняматриці.
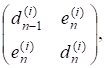
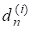
яке лежить ближче до. Крім методу явних зсувів для прискорення збіжності застосовується метод неявних зсувів, який, проте, виходить за рамки цієї книги.
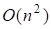
Для симетричних тридіагональних матриць потрібно виконати операцій, щоб відшукати кожне власне значення, отже операцій, щоб відшукати всі власні значення.
Крім власних значень, нас цікавлять також власні вектори, які для симетричних матриць можна знайти таким чином: якщо, то стовпчики матриці апроксимують власні вектори матриці, тобто .
Отже, для обчислення власних значень та власних векторів симетричної матриці можна запропонувати такийалгоритм.
1. Звести до тридіагонального вигляду.
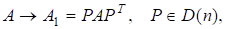
— симетрична і тридіагональна матриця;
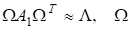
2. Знайти власні наближені значення за допомогоюалгоритму з поворотами Гівенса: добутком поворотів Гівенса.
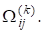
3. Стовпчики є апроксимаціями власних векторів :
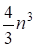
Цей алгоритм потребує ~ множень для перетворення до тридіагонального вигляду і для виконанняалгоритму. Для загальних матриць спочатку виконується перетворення до форми Хессенберга, а потім за допомогоюалгоритму — до нормальної форми Щура (комплексної верхньої трикутної матриці).