Застосування перетворення Фур'є

У наші дні вивчення даного процесу в основному зводиться до знаходження ефективних методів переходу від функції до її перетвореному увазі і назад. Таке рішення називається пряме і зворотне перетворення Фур'є. Що це означає? Для того щоб визначити інтеграл і провести пряме перетворення Фур'є, можна скористатися математичними методами, а можна і аналітичними. Незважаючи на те що при їх використанні на практиці виникають певні труднощі, більшість інтегралів вже знайдені і внесені в математичні довідники. За допомогою чисельних методів можна розраховувати вираження, форма яких грунтується на експериментальних даних, або функції, інтеграли яких в таблицях відсутні і їх складно уявити в аналітичній формі.

До появи обчислювальної техніки розрахунки таких перетворень були вельми нудними, вони вимагали ручного виконання великої кількості арифметичних операцій, які залежали від числа точок, що описують хвильову функцію. Для полегшення розрахунків сьогодні існують спеціальні програми, що дозволили реалізувати нові аналітичні методи (рис. 3, 4).

Так, в 1965 році Джеймс Кулі та Джон Тьюки створили програмне забезпечення, що здобуло популярність як «швидке перетворення Фур'є». Воно дозволяє економити час проведення розрахунків за рахунок зменшення числа множень при аналізі кривої. Метод «швидке перетворення Фур'є» заснований на поділі кривої на велике число рівномірних вибіркових значень. Відповідно кількість множень знижується вдвічі при такому ж зниженні кількості точок.

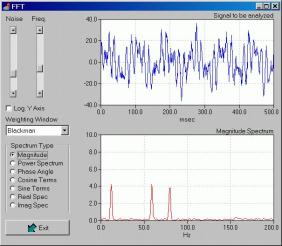
Рисунок 3. Програмне забезпечення для виконання швидкого перетворення Фур'є.

Даний процес використовується в різних областях науки: в теорії чисел, фізиці, обробці сигналів, комбінаторики, теорії ймовірності, криптографії, статистикою, океанології, оптиці, акустиці, геометрії та інших. Багаті можливості його застосування засновані на ряді корисних особливостей, які отримали назву «властивості перетворення Фур'є». Розглянемо їх.

• 1. Перетворення функції є лінійним оператором і з відповідною нормалізацією є унітарною. Дана властивість відомо як теорема Парсеваля, або в загальному випадку теорема Планшереля, або дуалізм Понтрягіна.
• 2. Перетворення є оборотним. Причому зворотний результат має практично аналогічну форму, як і при прямому рішенні.
• 3. Синусоїдальні базові вирази є власними диференційованими функціями. Це означає, що таке подання змінює лінійні рівняння з постійним коефіцієнтом у звичайні алгебраїчні.
• 4. Згідно з теоремою «згортки», даний процес перетворює складну операцію в елементарне множення.
• 5. Дискретне перетворення Фур'є може бути швидко розраховане на комп’ютері з використанням «швидкого» методу.