Критичні точки функції, максимуми і мінімуми

Важливо відзначити, що теорема Ферма є лише необхідну умову екстремуму: з того, що похідна в точці звертається в нуль, необов’язково випливає, що в цій точці функція має екстремум. Наприклад, похідна функції звертається в нуль у точці 0, але екстремуму в цій точці функція не має (рис. 105). Необхідна умова екстремуму. Якщо точка x0 є точкою екстремуму функції й у цій точці існує похідна, то вона… Читати ще >
Критичні точки функції, максимуми і мінімуми (реферат, курсова, диплом, контрольна)
Внутрішні точки області визначення функції, у яких її похідна дорівнює нулю або не існує, називаються критичними точками цієї функції. Ці точки відіграють важливу роль при побудові графіка функції, оскільки тільки вони можуть бути точками екстремуму функції (мал. 103 і 104). Сформулюємо відповідне твердження, його називають теоремою Ферма (на честь французького математика Пьера Ферма).

Необхідна умова екстремуму. Якщо точка x0 є точкою екстремуму функції й у цій точці існує похідна, то вона дорівнює нулю: .
Важливо відзначити, що теорема Ферма є лише необхідну умову екстремуму: з того, що похідна в точці звертається в нуль, необов’язково випливає, що в цій точці функція має екстремум. Наприклад, похідна функції звертається в нуль у точці 0, але екстремуму в цій точці функція не має (рис. 105).
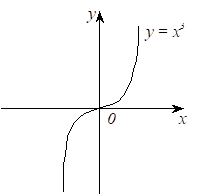
Рис. 105.
Дотепер ми розглядали критичні точки, у яких похідна дорівнює нулю. Розглянемо тепер критичні точки, у яких похідна не існує. (Відзначимо, що, наприклад, точка 0 для функції не є критичної: у ній похідна не існує, але вона не внутрішня точка області визначення.) У цих точках функція також може чи мати не мати екстремум.
З теореми Ферма випливає, що при знаходженні точок екстремумів функції потрібно в першу чергу знайти її критичні точки. Але, як видно з розглянутих прикладів, питання про тім, чи дійсно дана критична точка є точкою екстремуму, вимагає додаткового дослідження. При цьому часто допомагають такі достатні умови існування екстремуму в точці.
Ознака максимуму функції. Якщо функція неперервна в точці, а на інтервалі, то точка є точкою максимуму функції .
Зручно користатися спрощеним формулюванням цієї ознаки:
Якщо в точці похідна змінює знак із плюса на мінус, тобто точка максимуму.
Ознака мінімуму функції. Якщо функція неперервна в точці, а на інтервалі, то точка є точкою мінімуму функції .
Зручно користатися спрощеним формулюванням цієї ознаки:
Якщо в точці похідна змінює знак з мінуса на плюс, тобто точка мінімуму.
Приклад 3. Знайдемо точки екстремуму функції .
Похідна цієї функції, рівна, визначена у всіх точках і звертається в нуль у точках -1 і 1. У точці -1 похідна змінює знак з мінуса на плюс (при і при). У точці 1 похідна змінює знак із плюса на мінус. Користаючись ознаками максимуму і мінімуму, одержуємо, що точка -1 є точкою мінімуму, а точка 1 — точкою максимуму функції. Графік функції зображений на рисунку 108.
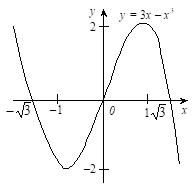
Рис. 108.