Основні теоретичні відомості з теорії кривих тривимірного евклідового простору

Нехай — тривимірний евклідів простір і G — зв’язна множина точок числової прямої (сегмент, напівcегмент, інтервал, відкрита або замкнута напівпряма, вся пряма). Векторною функцією (вектор — функцією), заданою на множині G, називається відображення, при якому кожному значенню відповідає вектор простору .

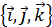
Зафіксуємо в деякий декартовий базис розкладемо вектор по цьому базису.

(t) = x (t) + y (t) + z (t) .

Скалярні функції x (t), y (t), z (t) називаються координатами векторної функції. Їхнє завдання рівносильне завданню векторної функції.

Постійний вектор називається границею векторної функції при, якщо для кожного е > 0 існує д > 0 таке, що для всіх, які задовольняють умові 0 < < d, виконується нерівність — | < е. Позначають: lim = .

Векторна функція називається неперервною в точці, якщо = lim. Якщо векторна функція неперервна в усіх точках множини G, то вона називається неперервною на цій множині.

Векторна функція називається диференційованою в точці, якщо при існує границя відношення.

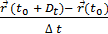
Ця границя називається похідною векторної функції в точці й позначається .

Очевидно, що для диференційованості функції в точці потрібна її неперервність у цій точці.

Якщо векторна функція диференційована в кожній точці множини G, то вона називається диференційованою на множині G .

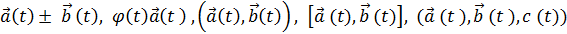
Нехай векторні функції і скалярна функція ц (t) диференційовані в точці, тоді в цій точці диференційовані функції і мають місце рівності:

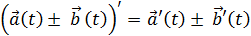
• 1. ,
• 2. ,
• 3. ,

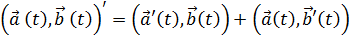
• 4. .
• 5.

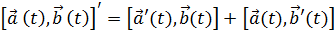
Якщо векторна функція має на множині G постійний модуль, то в кожній точці цієї множини вектор ортогональний похідній, яка обчислюється в цій точці.

Нехай скалярна функція диференційована в точці S, а векторна функція диференційована в точці t. Тоді складна.

диференційована в точці.

.

Параметризованою кривою, заданою на зв’язній множині називається неперервне відображення, при якому кожному значенню відповідає деяка точка простору. Змінна t називається параметром кривої. Образ множини I при відображенні г називається носієм кривої.

Зазначене у визначенні параметризованої відображення g є неперервною векторною функцією. У зв’язку із цим рівняння називають векторним рівнянням кривої, а рівняння.

параметричними рівняннями кривої. Говорять також, що крива задана за допомогою векторної функції r (t) і пишуть.

.

Будемо користуватися записом.

.

маючи на увазі, що точка M кривої є образом при відображенні. Крива г, задана за допомогою векторної функції називається гладкою кривою класу, де якщо векторна функція має неперервні похідні до порядку включно. Гладка крива класу називається регулярною в точці, якщо. Вектор називається вектором швидкості кривої у точці. Точка параметризованої кривої, у якій вектор швидкості нульовий, називається особливою точкою кривої, всі інші точки кривої називаються неособливими або звичайними.

Заміна параметра на кривій за законом.

називається припустимою, якщо функція в проміжку має неперервну похідну, що у всіх точках.

Для обчислення довжини використовується формула:

Параметризація кривої за допомогою довжини дуги, що відлічується від деякої точки кривої, називається природною або натуральною параметризацією.

Теорема 1. Параметризація кривої є природною тоді й тільки тоді, коли вектор швидкості кривої задовольняє умові .

Доведення. Нехай.

Тоді.

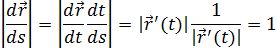
В іншу сторону. Нехай, й нехай.

(якщо це не так, можна зробити заміну параметра).

Виберемо 0 за початок відліку, тоді.

.

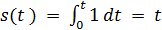
тобто параметр t є.

довжиною дуги кривої. Теорема доведена.

Щоб знайти натуральну параметризацію кривої, заданої векторним рівнянням, необхідно.

1. Знайти за формулою.

;

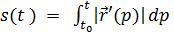
• 2. Виразити через ;
• 3. Підставити у векторне рівняння кривої .

Криву в можна визначити як множину точок, координати яких задовольняють системі рівнянь.

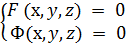
де F (х, y, z), Ф (х, y, z) — скалярні функції змінних х, y, z. Оскільки кожне рівняння системи задає в просторі поверхню, то крива є перетином поверхонь. Будемо називати такий спосіб завдання кривої неявним.

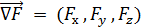
Вектор називається градієнтом функції F (х, y, z). Точка M неявно заданої кривої буде неособливою, якщо в ній вектор. Ця умова рівносильна наступній Нехай — фіксована точка регулярної кривої, M довільна точка цієї кривої. Граничне положення січної при прагненні точки M по кривій до точки називають дотичною прямою даної кривої у точці. Площина, що проходить через точку кривої.

перпендикулярно її дотичній прямій у цій точці, називається нормальною площиною кривої в даній точці.

Нехай — регулярна крива й точка.

належить цій кривій.

Вектор

є напрямним вектором дотичної прямої у точці та нормальним вектором нормальної площини, канонічні рівняння яких мають вигляд.

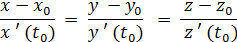
відповідно.

Для неявно заданої кривої в її неособливій точці.

рівняння дотичної прямої та нормальної площини мають вигляд.

.

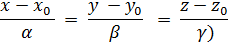
відповідно, де б, в, г — координати вектора.

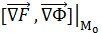
Стичною площиною просторової кривої в даній її точці називається граничне положення, до якого прагне січна площина (), за умови, що точки й прагнуть по кривій до точки .

Нехай дана гладка класу крива. Точка.

= називається бірегулярною точкою цієї кривої, якщо в ній виконана умова. У противному випадку точка M 0 називається точкою розпрямлення.

Усяка крива в будь-якій своїй бірегулярній точці = має стичну площину, нормальним вектором якої є вектор .

Головною нормаллю кривої в точці M називається пряма, що є перетином стичної і нормальної площин кривої у цій точці. Пряма, що проходить через точку M й перпендикулярна стичній площині, називається бінормаллю кривої в точці M. Площина, яка містить в собі дотичну пряму і бінормаль, називається спрямною площиною кривої.

Фігура, що складається із трьох прямих (дотичної, головної нормалі й бінормалі) і трьох площин (нормальної, стичної й спрямної), називається тригранником Френе.