Рівняння першої ступені з одним невідомим

Розглянемо рівняння першої степені з параметрами.

. (1).

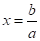
• 1. При рівняння має один розв’язок .
• 2. При рівняння не має розв’язків.
• 3. При кожне значення являється розв’язком рівняння. Розв’язок рівняння не єдине. Рівняння має безліч розв’язків.

Приклад. Знайдемо розв’язок лінійного рівняння.

.

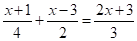
Приводимо рівняння до вигляду.

.

Приклад. Лінійне рівняння.

.

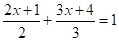
приводитися до вигляду Приклад. Розв’яжемо лінійне рівняння Рівняння має неєдиний розв’язок.

Лінійне рівняння (4) або має єдиний розв’язок, або нескінченну безліч розв’язків, або зовсім не має розв’язків.

Приклад. Режим лінійного рівняння.

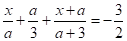
. (5).

При, рівняння передіятися до вигляду.

.

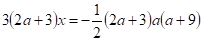
• 1. Якщо або, те рівняння (5) не має розв’язків.
• 2. Якщо, те, тобто .

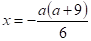
3. Якщо, ,, те .

Приклад. Знайти розв’язок рівняння.

(6).

.

• 1. Якщо, те рівняння (6) не має розв’язків.
• 2. Якщо, те, .

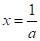
3. Якщо, , те .

У багатьох випадках систему лінійних алгебраїчних рівнянь можна звести до одного лінійного рівняння вигляду (4).

Приклад. Знайдемо розв’язок системі лінійних рівнянь.

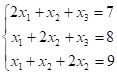
З першого рівняння знаходимо.

і підставимо в два інших рівняння. Отримаємо систему.

З першого рівняння знаходимо, і підставимо в останнє рівняння. Отримаємо одне рівняння з одним невідомим. З попередніх рівнянь знаходимо .

Аналогічно виключаються невідомі з системи лінійних алгебраїчних рівнянь з параметрами.

Приклад. Знайти значення параметра b, при якому система лінійних рівнянь.

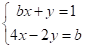
маємо нескінченно багато розв’язків. Крім невідомого, отримаємо рівняння При це рівняння, а отже і вихідна система лінійних рівнянь має нескінченно багато розв’язків.

Приклад. Знайти значення параметра, при якому система рівнянь.

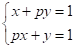
не має розв’язків. За винятком невідомого, приходимо до рівняння першого ступеня з одним невідомим.

.

При це рівняння вихідна система рівняння не має розв’язків.

Приклад. Знайти значення параметра, яку задовольняє наступній умові. Для будь-якого дійсного значення параметра знайдеться хоча б одне значення параметра таке, що задана система.

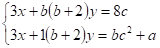
маємо хоча б один розв’язок.

Вилучимо із системи рівняння невідоме і приходимо до лінійного рівняння.

(7).

Якщо, те рівняння (7) має розв’язок за любимо. При або коефіцієнт при в рівняння (7) перетворюється в нуль. Щоб рівняння (7) мало розв’язок необхідно виконати умови.

.

При одному й тому ж значенні параметра, може бути, але при, різних значень параметра. Умови можливості параметра зводиться до нерівностей звідки знаходимо значення параметра .

Приклад. Знайдемо умови можливості розв’язання системи лінійних рівнянь.

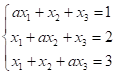
Складаючи всі рівняння системи, знаходимо.

.

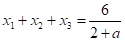
Віднімаючи з цього рівняння системи, знаходимо.

.

Цей розв’язок існує, якщо .

Вправи для розв’язування.

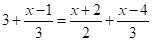
• 1. ;
• 2. ;
• 3. ;

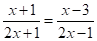
• 4. ;
• 5. ;
• 6. ;
• 7. ;
• 8. ;
• 9.

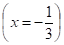
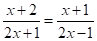
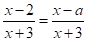
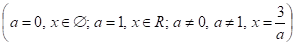
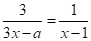
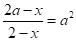
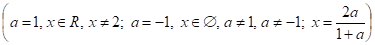
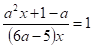
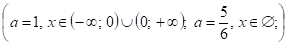
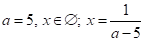
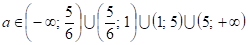
при ;

10. За яких значень параметра для довільного дійсного значення знайдеться хоча б одне дійсне значення параметра таке, що задана система рівнянь.

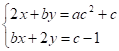
має хоча б один розв’язок.