До питання про розробку моделі нелінійного двополюсника з керованою вольт-амперною характеристикою

Аннотация: В данной работе рассматриваются вопросы разработки схемы замещения нелинейного двухполюсника с вольт-амперной характеристикой, управляемой напряжением, либо током, которую можно формировать, не изменяя схемы, в соответствии с требованиями проектирования. Для решения задачи используется аналого-цифро-аналоговый элемент. Вольт-амперная характеристика данного элемента определяется программой работы цифрового устройства. Для аппроксимации характеристик нелинейных элементов применяются полиномы различной степени — отрезки рядов Тейлора, Маклорена, Лагранжа и др. По нашему мнению решение подобной задачи является актуальным.

Ключевые слова: Синтез схемы, нелинейные цепи, эквивалентные преобразования, аналого-цифро-аналоговый элемент, нелинейное сопротивление, управляемый источник напряжения, ряд Тейлора.

Успехи современной микроэлектроники позволяют на более высоком уровне синтезировать устройства для решения задач моделирования, автоматического управления, связи и т. п.

Подавляющее большинство физических процессов являются нелинейными. В данной работе рассматриваются только такие процессы, которые могут быть описаны соответствующими нелинейными алгебраическими или нелинейными интегрально — дифференциальными уравнениями. Будем полагать так же, что существуют электрические цепи, токи и напряжения которых с точностью до обозначений совпадают с соответствующими физическими величинами. Полученная таким образом модель представляет собой некоторую нелинейную электрическую цепь, которая, в общем случае, состоит из линейной части, в которой могут процессы преобразования, накопления электрической энергии, а также процессы обратимости [1] и нелинейной части. В работах [2 — 5] показано, что существуют классы схем замещения электрических цепей, которые путём эквивалентных и квазиэквивалентных преобразований могут быть сведены к нелинейным схемам замещения с нелинейными резисторами. Подобные схемы замещения можно представить так, как показано на рис. 1.

нелинейный двухполюсник вольт амперный Будем полагать так же, что нелинейная часть состоит только из двухполюсных элементов, и что вольт-амперная (ампер-вольтная) характеристики каждого элемента известны. Основная проблема реализации двухполюсников с заданными вольт-амперными характеристиками состоит в большом многообразии характеристик и в технической сложности достижения, например [6, 7] их точности и стабильности. Эти недостатки присущи многим известным методам [2 — 5, 8 — 10]. В результате, как правило, при реализации устройств, содержащих нелинейные элементы, требуется выполнение этапа настройки.

Целью данного исследования является разработка схемы замещения нелинейного двухполюсника с управляемой либо напряжением, либо током вольт-амперной характеристикой, которую можно формировать, не изменяя схемы, в соответствии с требованиями проектирования. По нашему мнению решение подобной задачи является актуальным.

В основе решения поставленной задачи лежит использование аналого — цифро-аналогово элемента [8]. Этот элемент представляет собой управляемый источник напряжения (рис.2).

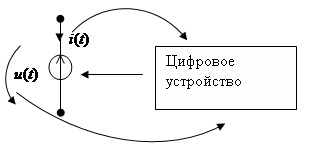
Рис. 2. — Аналого-цифро-аналоговый элемент

Вольт амперная характеристика данного элемента определяется программой работы цифрового устройства. Таким образом, не меняя конструкции устройства на рис. 2, используя только программные средства, можно получать элементы с различными вольт-амперными характеристиками. В настоящее время для аппроксимации характеристик нелинейных элементов широко применяются полиномы различной степени (отрезки рядов Тейлора, Маклорена, полиномы Лагранжа и др.) [2, 3, 10]. Схема замещения нелинейного элемента, полюсное уравнение которого имеет вид полинома, может быть представлена так, как показано на рис. 3.

При выбранном способе аппроксимации полюсное уравнение k-го элемента на рис. 3 имеет вид:

(1).

где вещественные числа; - номер по порядку.

Будем синтезировать схему каждого элемента на рис. 3 схемой, приведенной на рис. 2. Выражение (1) можно рассматривать как решение некоторого дифференциального уравнения. В таком случае числа можно рассматривать как постоянные интегрирования. Так как в выражении (1) два постоянных числа (две постоянных интегрирования), то искомое дифференциальное уравнение является дифференциальным уравнением второго порядка. Продифференцируем уравнение (1) дважды.

(2).

. (3).

Рассматривая уравнения (1), (2) и (3) как систему уравнений, исключим постоянные интегрирования из уравнения (3).

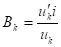
. (4).

Если разделить (3) на (2), то с учётом (4) получим:

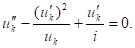
(5).

Полученное уравнение и есть полюсное уравнение k-го элемента в схеме на рис. 3, записанное в дифференциальной форме.

Для того, чтобы постоянные интегрирования удовлетворяли заданным условиям (1), необходимо обеспечить начальные условия, удовлетворяющие уравнениям (6) и (7):

. (6).

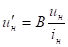
. (7).

В тех случаях, когда один из коэффициентов, А или В не должны изменяться в зависимости от начальных условий, можно ограничиться при моделировании дифференциальным уравнением первого порядка. Например, пусть коэффициент В не должен изменяться в зависимости от начальных условий. Тогда в выражении (1) можно считать постоянной интегрирования только коэффициент А. Из (1) следует:

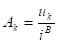
. (8).

Дифференцируя (1) по току, получим:

. (9).

С учётом выражения (8) соотношение (9) может быть преобразовано к виду:

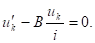
(10).

Постоянная интегрирования в решении уравнения (10) находится из начальных условий.

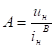
. (11).

По данной работе можно сделать следующие выводы:

• 1. При моделировании нелинейных вольт-амперных характеристик полиномами схему замещения каждого нелинейного элемента можно представить как последовательное соединение соответствующих аналого-цифро-аналоговых двухполюсников.
• 2. Полюсное уравнение каждого двухполюсника может быть записано в дифференциальной форме (5) или (10).
• 3. Соотношения (5) или (10) являются основой для составления алгоритма работы цифрового устройства (рис.2).
• 4. В общем случае математическое уравнение, описывающее вольт-амперную характеристику нелинейного резистивного двухполюсника, может содержать большее количество постоянных коэффициентов (например, n). Тогда полюсное уравнение такого элемента будет представлять собой дифференциальное уравнение n-го порядка.
• 5. Наличие цифровой части в аналого-цифро-аналоговом элементе позволяет отладку радиоэлектронной аппаратуры выполнять только программными средствами и отказаться от подбора параметров аналоговых элементов.

• 1. Пивнев В. В., Басан С. Н. Некоторые аспекты обратимости процессов в линейных электрических цепях второго порядка // Инженерный вестник Дона, 2013, № 4 URL: ivdon.ru/magazine/archive/n4y2013/1969/.
• 2. Филиппов Е. Нелинейная электротехника. М.: Энергия, 1968. 503 с.
• 3. Данилов Л. В., Матханов П. Н., Филиппов Е. С. Теория нелинейных электрических цепей. Ленинград: Энергоатомиздат, 1990. 252 с.
• 4. Данилов Л. В. Электрические цепи с нелинейными R элементами. М.: Связь, 1974. 135 с.
• 5. Басан С. Н. Электрические цепи с нелинейными резисторами. Ростов-на-Дону: Издательство Ростовского университета, 1984. 200 с.
• 6. Пилипенко А. М., Бирюков В. Н. Моделирование параметров МОП-транзисторов в широком температурном диапазоне // Инженерный вестник Дона, 2013, № 4 URL: ivdon.ru/magazine/archive/n4y2013/1917/.
• 7. Богданов С. А. Влияние неоднородного распределения электрически активных примесей на перенос носителей заряда в контактах металл-полупроводник с барьером Шотки // Инженерный вестник Дона, 2013, № 3 URL: ivdon.ru/magazine/archive/n3y2013/1822/.
• 8. Басан С. Н., Изотов М. В. Универсальный аналого — цифровой элемент электронной техники // Труды международной научной конференции. ТаганрогДивноморск: 2009. С. 486−489.
• 9. Pivnev V.V., Basan S.N. Some questions about equivalent circuit synthesis and nonlinear electrical circuit implementation with the specified properties in the electronic simulation tasks // Applied Mechanics and Materials Vols. 670−671. 2014. pp. 1454−1457.
• 10. Pivnev V.V., Basan S.N. Some the application of the Taylor series for the analysis of processes in non-linear resistive circuits // Applied Mechanics and Materials Vols. 701−702. 2015. pp. 1173−1176.