Синтез корегуючих пристроїв методом ЛАХ

Одним з найефективніших методів синтезу систем автоматичного керування є метод, в основу якого покладено використання ЛАХ розімкнутої системи. Ідея методу ґрунтується на тому, що для стійких мінімально-фазових систем існує однозначний зв’язок між перехідною характеристикою замкнутої системи і виглядом ЛАХ відповідної розімкнутої системи. Виходячи з бажаного вигляду перехідного процесу, будують ЛАХ, яка відповідає такому процесу.

Далі, знаючи вигляд бажаної ЛАХ, до неї наближують ЛАХ вихідної системи, запроваджуючи різні корегуючи пристрої.

Будь-яка САК з електроприводом складається з незмінної частини, до якої належать: об'єкт регулювання, електродвигун, силовий керований перетворювач, а також елементи головного зворотного зв’язку та порівняння.

Об'єкт регулювання вважається відомим при проектуванні САК, двигун і перетворювач вибирають, виходячи з технологічних характеристик об'єкта. Природно, що ці елементи не підлягають зміні при корекції динамічних властивостей САК. Незмінними звичайно також вважаються елементи, що забезпечують потрібну точність роботи системи в уставленому режимі - підсилювач, а в астатичній системі - інтегруючий елемент. Елементи САК, що не змінюються, визначають ЛАХ вихідної (нескорегованої) системи. Бажану ЛАХ, яка визначає потрібну якість САК. Умовно поділяють на три частини: низькочастотну Lн.ч.(щ), середньочастотну Lс.ч.(щ), високочастотну Lв.ч.(щ). Можливий вигляд бажаної ЛАХ показано графічно.

До низькочастотної частини ЛАХ належить ділянка характеристики, нахил якої не змінюється при. Вона проходить через точку з координатами, де k — коефіцієнт передачі розімкнутої системи, і має нахил 0 ДБ/дек для статичних систем, — 20 ДБ/дек — для астатичних систем першого порядку, — 40 ДБ/дек — для астатичних систем другого порядку.

Низькочастотна частина ЛАХ визначається коефіцієнтом передачі розімкнутої системи k і порядком астатизму, отже вона характеризує точність роботи системи в установлених режимах. Якщо до незмінюваної частини системи належать елементи, що забезпечують потрібну точність роботи САК в установленому режимі, то низькочастотні частини бажаної ЛАХ і ЛАХ вхідної системи збігаються.

До середньочастотної частини належить ділянка ЛАХ з однаковим нахилом, що проходить через частоту зрізу щ3. Ця частина ЛАХ є найважливішою, бо вона визначає переважно якість перехідних процесів. Основними параметрами, які характеризують середньочастотну частину, є її нахил і частота зрізу. Для задовільної якості перехідних процесів замкнутої системи необхідно, щоб нахил ЛАХ на частоті зрізу дорівнював — 20 ДБ/дек. Якщо нахил на частоті зрізу становить — 40 ДБ/дек, то перехідний процес має велике перерегулювання, а при нахилі - 60 ДБ/дек система, як правило буде нестійкою. Частота зрізу щ3 визначає швидкодію САК. Швидкодія зростає при збільшенні щ3.

Високочастотна частина ЛАХ Lв.ч.(щ) знаходиться в зоні від'ємних децибелів, тому майже не позначається на якості перехідного процесу і впливає лише на його початок. Краще мати якомога більший нахил асимптот високочастотної частини, бо це зменшує вплив високочастотних перешкод.

Для побудови бажаної ЛАХ, виходячи із заданих вимог до якості перехідних процесів, використовують різні методи. Розглянемо найпоширеніші з них.

Метод В.В. Солодовнікова

Розглянемо цей метод стосовно астатичної системи першого порядку, в якої низькочастотні асимптоти з нахилом — 20 ДБ/дек вихідної Lв.(щ) і бажаної ЛАХ Lб(щ) збігаються і проходять через точку з координатами L (щ)=20lgk, lgщ=0.

Вихідними даними для побудови бажаної ЛАХ є час регулювання tp перерегулювання у. Можуть бути задані також максимальне прискорення amax та початкове розходження вихідної координати x0. Бажану ЛАХ Lб (щ) будують у такій послідовності.

1. Вибираємо частоту зрізу, виходячи з умови.

щ31?щ3?щ32, де.

щ31 — мінімальне значення частоти зрізу, при якому час регулювання не перевищує заданий.

щ32 — максимальне значення частоти зрізу, яке визначають, виходячи із заданого максимального прискорення x0.

Значення щ31 визначають за монограмою у такому порядку.

Виходячи із заданого значення у, за графіком у (Umax) визначають відповідне значення Umax. Потім за цим значенням Umax за графіком tp (Umax) знаходять ср/щ31. Цю величину порівнюють із заданим значенням tp і із знайденого рівняння визначають.

;

Частоту щ32 обчислюють за формулою.

Якщо щ31>щ32, то слід вибрати щ3?щ32. Якщо значення amax і x0 не задані, то щ3?щ31 .

2. Після визначення частоти зрізу будують середньочастотну асимптоту бажаної ЛАХ, яка проходить через частоту зрізу з нахилом — 20 Дб/дек.

• 3. За графіком, виходячи із знайденого значення Umax визначають LДц і Дцmin.
• 4. Після цього сполучають середньочастотну асимптоту з низькочастотною так, щоб в інтервалі частот, для якого 0?Lу (щ)?LДц надлишок фази був більшим або дорівнював мінімальному надлишку:

Дц?Дцmin (**).

Сполучення здійснюють асимптотою з нахилом — 40 Дб/дек або — 60 Дб/дек для систем першого порядку і - 60 Дб/дек для систем другого порядку.

Надлишок фази при частоті ща можна визначити за такою наближеною формулою :

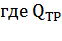
, де.

н — порядок астатизму ;

щі — частоти сполуки бажаної ЛАХ, які містяться ліворуч від ща;

m і l — кількість частот сполуки, на яких нахил бажаної ЛАХ змінюється на — 20 Дб/дек або + 20 Дб/дек відповідно.

Надлишок фази, де ц (щ)<0, перевіряють лише для тієї частоти ща (див рис.*), для якої Lб (щ) =LДц. Частоті ща може відповідати точка сполуки асимптот або точка на одній з цих асимптот.

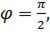
Задоволення умов (*) і (**) означає, що бажаній ЛАХ відповідає типова частотна характеристика U (щ), у якої і для якої складено використані раніше залежності у (Umax) і tp (Umax).

Якщо на частоті ща надлишок фази Дца<�Дцmin, то асимптоту сполуки необхідно зсунути вліво або збільшити її нахил. Отже, потрібне положення асимптоти сполуки відбувається методом спроб. При цьому різниця ДцаДцmin не повинна перевищувати кількох градусів.

5. Середньочастотну асимптоту сполучають з високочастотною так, щоб в інтервалі частот, для якого 0? Lб (щ)?LДц надлишок фази становив Дц? Дцmin.

Надлишок фази досить перевірити при частоті щу (див рис. *) за такою наближеної формою:

qсер — відносний нахил середньо частотної асимптоти (при нахилі - 20 Дб/дек qсер =2).

r — кількість частот сполуки бажаної ЛАХ, що перевищують частоту зрізу щ3 ;

щі — частоти сполуки бажаної ЛАХ, що перевищують щ3;

Якщо Дц<�Дцmin; то асимптоту сполуки треба зсунути вправо або зменшити її нахил, якщо Дц>Дцmin — то зсунути вліво або зменшити її нахил. Дц — Дцmin не повинна перевищувати кількох градусів.

При сполученні середньочастотної частини ЛАХ з низькочастотною та високочастотною слід прагнути до того, щоб бажана ЛАХ якомога менше відрізнялась від ЛАХ вихідної системи. Це спрощує корекцію.

Метод Санковського — Сігалова

В основу цього методу покладено дев’ять типів бажаних ЛАХ розімкнутої системи, які наведені в довідковій літературі.

Той чи інший тип ЛАХ вибирається залежно від вимог до САК, що синтезуються. Ці вимоги є вихідними даними для синтезу.

До них належать:

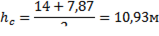
— максимальне значення швидкості та прискорення зміни завдання.

tp — час регулювання;

у — перерегулювання.

При виборі ЛАХ рекомендується керуватися такими положеннями:

• 1) якщо завдання змінюється з великим прискоренням, а рівень перешкод незначний, то слід вибирати ЛАХ типу 1 для статичних систем і типу 2 для астатичних.
• 2) якщо прискорення з яким змінюється завдання невелике, але рівень перешкод досить значний, то слід вибирати ЛАХ типів 3, 4 або 5.
• 3) при великих прискореннях зміни завдання і значному рівні перешкод треба вибирати ЛАХ типів6, 7, 8 або 9.

У всіх інших випадках при виборі бажаної ЛАХ слід прагнути до того, щоб бажана ЛАХ якомога менше відрізнялася від ЛАХ вихідної системи.

Після того, як тип бажаної ЛАХ вибрано і, виходячи з вимог до якої САК в установленому режимі, визначено її низькочастотну частину, для побудови решти частин бажаної ЛАХ використовують дані таблиці і такі співвідношення:

частота зрізу.

(*).

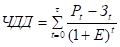
запас стійкості по фазі.

Дц0 =73-у (**).

де с=9 при Дц=300;с=8 при Дц=450 і с=7 при Дц=600

Формули (*) (**) дають похибку, що не перевищує 0,05 0,1 при 600>Дц>300/.

При розрахунках можна користуватися й такими співвідношеннями:

;

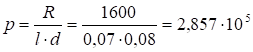
де.

l=2 або 3 при нахилі асимптоти, що сполучає середньота низькочастотні частини ЛАХ, — 40 Дб/дек, або — 60 Дб/дек ;

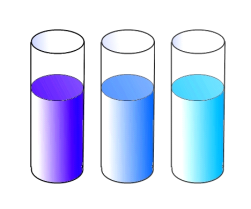
Значення а (у радіанах) визначають, виходячи з припущення, що.

при і=3,4…

.

Спрощена побудова бажаної ЛАХ

Вихідними даними для побудови Lу (щ) є час регулювання tp та перерегулювання у. Частота зрізу бажаної ЛАХ обчислюється за формулою:

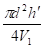
де.

k0 — коефіцієнт, що визначається за графіком залежно від перерегулювання.

k0=f (у)(по даному графіку).

Для у=1530% вибираємо k0=1,32,5 або по графіку.

Через частоту зрізу щзр проводиться середньочастотна асимптота бажаної ЛАХ з нахилом -20 Дб/дек частоти щ2 і щ3, що обмежують середньочастотну асимптоту ліворуч і праворуч вибирають виходячи з таких наближених рівностей.

.

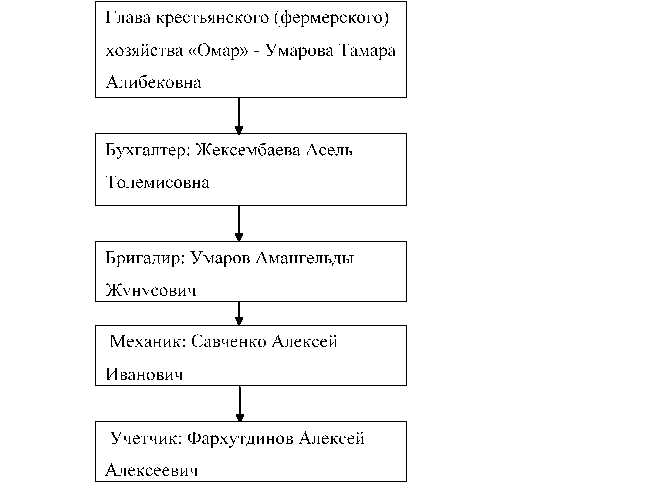
Для наближеної, але досить точної оцінки показників якості перехідного процесу можна використати графіки (див. літературу).

Перерегулювання у визначається за графіком залежно від коефіцієнтів а2 і а3, що визначають довжину середньочастотної частини ЛАХ:

; .

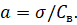
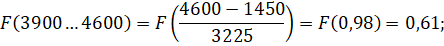
Запас стійкості по фазі Дц визначається за графіком в залежності від перерегулювання.

Синтез послідовної корегуючої ланки

Послідовна корегуюча ланка вводиться в основний контур регулювання системи і звичайно є пасивним чотириполюсником або регулятором на базі операційного підсилювача.

По можливості ланку слід вводити ближче до входу системи, де сигнали мають найменшу потужність. Передаточна функція вихідної розімкнутої системи.

Після введення корегуючої ланки матиме вигляд Після переходу до логарифмічних характеристик дістанемо.

.

Звідки.

Цей вираз визначає такий порядок синтезу послідовної корегуючої ланки:

• 1) виходячи із заданої структури системи і параметрів її ланок будують ЛАХ вихідної розімкнутої системи;
• 2) за заданими показниками якості будують бажану ЛАХ ;
• 3) визначають ЛАХ корегуючої ланки як різницю;
• 4) за ЛАХ корегуючої ланки визначають її передаточну функцію, схему і її параметри.

Синтез паралельної корегуючої ланки

Паралельні корегуючі ланки вводять у вигляді зворотних зв’язків, які охоплюють одну або кілька ланок вихідної системи.

Термін «паралельна корегуюча ланка» тут не зовсім точний, через те, що корегуюча ланка вмикається не паралельно ланкам системи, а створює від'ємний зворотній зв’язок. Передаточна функція вихідної розімкнутої системи має вигляд:

.

де — передаточна функція частини системи, що охоплюється паралельною корегуючою ланкою;

— передаточна функція решти частин розімкнутої системи.

;

.

Після введення корегуючої ланки передаточна функція системи має вигляд. автоматизований диференціальний регулятор дискретний.

(*).

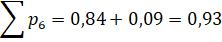
Після переходу до логарифмічних характеристик дістанемо :

(**).

Основна складність синтезу паралельної корегуючої ланки зумовлена наявністю одиниці у знаменнику передаточної функції (*). Для подолання цього іноді розглядається тільки інтервал частот, у якому:

тобто одиницю в знаменнику взагалі не враховують. Проте ця нерівність виконується тільки для високих частот і не зберігається на низьких частотах.

Розглянемо досить точний метод синтезу, який дозволяє враховувати одиницю в знаменнику передаточної функції. Введемо такі позначення:

(***).

і відповідно.

;

За формулою (**) будуємо ЛАХ L11(щ), віднявши Lу (щ) від Lв (щ). Залишається перейти від L11(щ) до L12(щ).

Цей перехід можна здійснити так. Виходячи з вигляду L11(щ), визначаємо W11(p) і відповідно до виразу (***) знаходимо передаточну функцію W12(p)=W11(p)-1, за якою будуємо ЛАХ L12(щ). ЛАХ L11(щ) вибирають по таблицям (див. літер.).

Після цих зауважень можна запропонувати такий порядок синтезу паралельної корегуючої ланки.

• 1. За заданою структурною схемою і параметрами її ланок будуються ЛАХ вихідної розімкнутої системи Lв (щ).
• 2. За заданими показниками якості будується бажана ЛАХ Lу (щ).
• 3. Відніманням бажаної ЛАХ Lу (щ) від ЛАХ вихідної системи Lв (щ) визначається ЛАХ

L11(щ)=Lв (щ)-Lу (щ) .

4. За виглядом L11(щ) і будується L12(щ) знаменника передаточної функції (*) без одиниці. У діапазоні частот, де виконується умова L11(щ>11ДБ ЛАХ L11(щ) і L12(щ) збігаються з точністю до 3ДБ. Якщо вважати цю точність достатньою, то перехід від L11(щ) до L12(щ) при L11(щ)>11ДБ не потребує ніяких перетворень. Для переходу від L11(щ) до L12(щ) у діапазоні частот, де L11(щ)<11ДБ, слід користуватися таблицями.

Після побудови L12(щ) необхідно перевірити стійкість внутрішнього контуру системи, який утворюється ланками з передаточною функцією WOX (р) і корегуючою ланкою. Висновок про стійкість внутрішнього контуру можна зробити лише за виглядом L12(щ).

• 5. Вибирається місце введення корегуючої ланки і будується LОХ (щ). Звичайно, корегуючою ланкою доцільно охоплювати частину системи, яка має великий коефіцієнт підсилення.
• 6. Визначається ЛАХ корегуючої ланки LК (щ) як різниця характеристик

L12(щ) і LОХ (щ):

LК (щ)=L12(щ)-LОХ (щ)

7. За виглядом ЛАХ корегуючої ланки визначається її передаточна функція, вибирається схема і обчислюються її параметри.

За допомогою ЛАХ можна синтезувати не тільки одну, а й кілька корегуючих ланок для однієї схеми: як послідовні корегуючі ланки, так і паралельні корегуючі ланки (по табл. підбір пасивні чотириполюсники).