Нейронна мережа зустрічного розповсюдження

Мета роботм: Вивчити архітектуру та принципи функціонування мережі зустрічного розповсюдження. Побудувати модель мережі зустрічного розповсюдження за допомогою пакету Neural Networks Toolbox, що входить до складу системи MATLAB.

Теоретичні відомості:

Принципи функціонування і навчання мережі зустрічного розповсюдження

Роберт Хехт-Нільсен (Robert Hecht-Nielsen) розробив мережу зустрічного розповсюдження (СounterРropagation) як засіб для поєднання неконтрольованого прошарку Кохонена із контрольованим вихідним шаром. Мережа призначена для вирішення складних класифікацій, при мінімізації числа нейронів та часу навчання.

Навчання для мережі СounterРropagation схоже на мережі з квантуванням навчального вектора. Приклад мережі зображений на рис. 4.1. Односкерована мережа CounterPropagation має три прошарки: вхідний шар, самоорганізована карта Кохонена та вихідний прошарок, що використовує правило «дельта» для зміни вхідних ваг з'єднань. Цей шар називають шаром Гросберга.

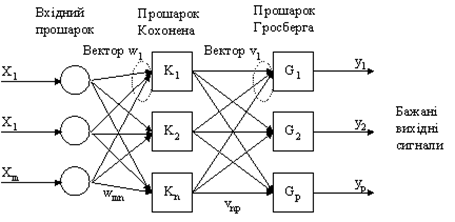
Рис. 4.1 — Мережа зустрічного поширення без зворотних зв’язків

Перша мережа СounterРropagation складалася з двоскерованого відображення між вхідним і вихідним шарами. Дані надходять на вхідний прошарок для генерації класифікації на вихідному прошарку, вихідний прошарок по черзі приймає додатковий вхідний вектор і генерує вихідну класифікацію на вхідному прошарку мережі. Через такий зустрічно-поширений потік інформації мережа отримала свою назву. Багато розробників використовують односпрямований варіант СounterРropagation, коли існує лише один шлях прямого поширення від вхідного до вихідного прошарку.

У мережі зустрічного поширення об'єднані два алгоритми: самоорганізована карта Кохонена і зірка Гросберга (Grossberg Outstar). Нейронні мережі, об'єднуючі різні нейропарадігмі як будівельні блоки, більш близькі до мозку по архітектурі, ніж однорідні структури. Вважається, що в мозку саме каскадні з'єднання модулів різної спеціалізації дозволяють виконувати необхідні обчислення. Кожен елемент вхідного сигналу подається на всі нейрони прошарку Кохонена. Ваги зв’язків (wmn) утворюють матрицю W. Кожен нейрон прошарку Кохонена з'єднаний з усіма нейронами шару Гросберга. Ваги зв’язків (vnp) утворюють матрицю ваг V.

У процесі навчання мережі зустрічного поширення вхідні вектори асоціюються з відповідними вихідними векторами (двійковими або аналоговими). Після навчання мережа формує вихідні сигнали, що відповідають вхідним сигналам. Узагальнююча здатність мережі дає можливість одержувати правильний вихід, якщо вхідний вектор неповний чи спотворений.

Навчання мережі. В результаті самонавчання прошарок здобуває здатність розділяти несхожі вхідні вектори. Який саме нейрон буде активуватися при пред’явленні конкретного вхідного сигналу, заздалегідь важко передбачити.

При навчанні прошарку Кохонена на вхід подається вхідний вектор і обчислюються його скалярні добутки з векторами ваг всіх нейронів.

Скалярний добуток є мірою подібності між вхідним вектором і вектором ваг. Нейрон з максимальним значенням скалярного добутку «переможцем» і його ваги підсилюються (ваговий вектор наближається до вхідного). wн = wc + r (x-wc) де wн — нове значення ваги, що з'єднує вхідний компонент x з нейроном, wс — попереднє значення ваги, r — коефіцієнт швидкості навчання, яке спочатку звичайно дорівнює 0.7 і може поступово зменшуватися в процесі навчання. Це дозволяє робити великі початкові кроки для швидкого грубого навчання і менші кроки при підході до остаточної величини.

Кожна вага, пов’язана з нейроном-переможцем Кохонена, змінюється пропорційно різниці між його величиною і величиною входу, до якого він приєднаний. Напрямок зміни мінімізує різницю між вагою і відповідним елементом вхідного шару.

Навчальна множина може містити багато подібних між собою вхідних векторів, і мережа повинна бути навченою активувати один нейрон Кохонена для кожного з них. Ваги цього нейрона є усереднення вхідних векторів, що його активують.

Виходи прошарку Кохонена подаються на входи нейронів прошарку Гросберга. Входи нейронів обчислюються як зважена сума виходів прошарку Кохонена. Кожна вага коректується лише в тому випадку, якщо вона з'єднана з нейроном Кохонена, що має ненульовий вихід. Величина корекції ваги пропорційна різниці між вагою і необхідним виходом нейрона Гросберга. Навчання шару Гросберга — це навчання «з вчителем», алгоритм використовує задані бажані виходи.

Функціонування Мережі. У своїй найпростішій формі прошарок Кохонена функціонує за правилом «переможець отримує все». Для даного вхідного вектора один і тільки один нейрон Кохонена видає логічну одиницю, всі інші видають нуль. Шар Гросберга функціонує в схожій манері. Його вихід є зваженою сумою виходів прошарку Кохонена. Якщо прошарок Кохонена функціонує так, що лише один вихід дорівнює одиниці, а інші дорівнюють нулю, то кожен нейрон шару Гросберга видає величину ваги, що зв’язує цей нейрон з єдиним нейроном Кохонена, чий вихід відмінний від нуля.

У повній моделі мережі зустрічного поширення є можливість одержувати вихідні сигнали по вхідним і навпаки. Цим двом діям відповідають пряме і зворотне поширення сигналів.

Області застосування. Розпізнавання образів, відновлення образів (асоціативна пам’ять), стиснення даних (із втратами).

Недоліки. Мережа не дає можливості будувати точні апроксимації (точні відображення). У цьому мережа значно уступає мережам зі зворотним поширенням похибки. До недоліків моделі також варто віднести слабкий теоретичний базис модифікацій мережі зустрічного розповсюдження.

Переваги:

• 1. Мережа зустрічного поширення проста. Вона дає можливість отримувати статистичні властивості з множини вхідних сигналів. Кохонен довів, що для навченої мережі імовірність того, що випадково обраний вхідний вектор буде найближчим до будь заданого вагового вектора, дорівнює 1 / k, k — число нейронів Кохонена.
• 2. Мережа швидко навчається. Час навчання в порівнянні зі зворотним поширенням може бути в 100 разів менше.
• 3. По своїх можливостях будувати відображення мережа зустрічного поширення значно перевершує одношарові перцептрони.
• 4. Мережа корисна для застосувань, де потрібна швидка початкова апроксимація.
• 5. Мережа дає можливість будувати функцію і зворотну до неї, що знаходить застосування при вирішенні практичних завдань.

Модифікації. Мережі зустрічного поширення можуть розрізнятися способами визначення початкових значень синаптичних ваг.

• 1. Для підвищення ефективності навчання застосовується додавання шуму до вхідних векторів.
• 2. Ще один метод підвищення ефективності навчання — надання кожному нейрону «почуття справедливості». Якщо нейрон стає переможцем частіше, ніж 1 / k (k — число нейронів Кохонена), то йому тимчасово збільшують поріг, даючи тим самим навчатися й іншим нейронам.
• 3. Крім «методу акредитації», при якому для кожного вхідного вектора активується лише один нейрон Кохонена, може бути використаний «метод інтерполяції», при використанні якого ціла група нейронів Кохонена, що мають найбільші виходи, може передавати свої вихідні сигнали в шар Гросберга. Цей метод підвищує точність відображень, реалізованих мережею.