Випадкові процеси в САК

Уявлення про випадкові процеси

При вивченні попереднього матеріалу припускалось, що всі дії, прикладені до САК, є детермінованими, тобто становлять цілком визначені функції часу. Практично ж САУ часто працюють в умовах, коли зовнішні дії мають випадковий характер. Як приклад таких дій можна навести опір руху електромеханічних об'єктів, коливання напруги живлення джерел енергопостачання електроприводів, випадкові перешкоди в регуляторах та вимірювальних пристроях. В слідкуючих системах дуже часто є випадковою також задаюча дія.

САК, що працюють в умовах випадкових збурень, можна проектувати, виходячи тільки з максимально можливих значень цих збурень.

Випадковою називається величина, значення якої визначається неконтрольованими причинами і тому не може бути точно передбаченою. Якщо випадкова величина може набувати окремих значень лише із скінченної множини її можливих значень, то вона називається дискретною випадковою величиною. Якщо ж випадкова величина може набувати усі значення в певному заданому інтервалі, то вона називається безперервною випадковою величиною. Ймовірність того, що безперервна випадкова величина набуде конкретного, заздалегідь визначеного значення, нескінченно мала, тобто ймовірність цієї події .

Найважливішими ймовірнісними характеристиками безперервних випадкових величин є функція розподілу, щільність розподілу, математичне очікування, дисперсія.

Функцією розподілу ймовірностей випадкової величини називається функція яка дорівнює ймовірності того, що випадкова величина має значення менше за . Ймовірність того, що безперервна випадкова величина потрапить у деякий проміжок, визначається різницею функцій розподілу, тобто Похідна від функції розподілу.

називається щільністю розподілу, або диференціальною функцією розподілу.

Математичне очікування, або середнє значення безперервної випадкової велечин, яке визначається за множиною її можливих значень, виражається через щільність розподілу за формулою.

а середнє значення квадрата безперервної випадкової величини — за формулою:

У цих формулах символ усереднення.

Випадкова величина , що змінюється в часі t, становить випадковий процес. Інакше кажучи, випадковий процес — це функція часу, значення якої в кожний момент часу є випадковою величиною. Отже, випадковий процес — це сукупність множини можливих кривих x (t), кожна з яких становить лише реалізації випадкового процесу x (t). Можливі графіки випадкових процесів мають вигляд:

У кожний окремий момент часу можна розглядати випадкові величини кожна з яких має свою функцію розподілу. Для випадкової величини функція розподілу має вигляд:

.

Функція називається одновимірною функцією розподілу ймовірностей випадкового процесу. Частинна похідна від неї.

.

називається одновимірною щільністю розподілу.

Випадкові процеси можуть бути стаціонарними або нестаціонарними. Якщо ймовірнісні характеристики випадкового процесу не залежать від вибору моменту часу t, тобто інваріантні відносно початку відліку, то випадковий процес називається стаціонарним. Графік випадкового стаціонарного процесу:

Стаціонарні випадкові процеси мають дуже важливу властивість, яка називається ергодичною властивістю. Її суть така: будь-яке середнє за множиною з ймовірністю «одиниця» (практично достовірно) дорівнює відповідному середньому за часом, тобто.

де рискою позначено усереднення за часом. Далі користуватимемося загальним символом усереднення , яким позначатимемо усереднення за множиною або за часом, тобто.

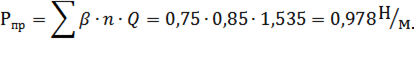
Замість терміну «випадковий» вживають також терміни стохастичний або ймовірнісний.

До основних характеристик стаціонарних випадкових процесів належать математичне очікування, дисперсія, кореляційні функції.

Математичне очікування визначає середнє значення випадкового процесу за множиною:

Дисперсія.

.

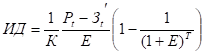
Квадратний корінь з дисперсії визначає середньоквадратичне відхилення.

.

Кореляційна функція (або автокореляційна) характеризує ступінь залежності (кореляції) між значеннями процесу, віддаленими один від одного на час, тобто оцінює швидкість змінювання випадкового процесу протягом часу. Вона становить середнє значення добутку випадкових процесів і визначається за формулою.

.

Для стаціонарного випадкового процесу кореляційна функція становить універсальну характеристику. Її можна досить просто обчислити, якщо мати експериментально зняті криві, тобто окремі реалізації випадкового процесу.

Одну з таких реалізацій зображено на графіку:

Для неї, згідно з виразом (*),.

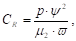
Чим більше час T і чим більше експериментально знятих кривих, тим точніше можна визначити кореляційну функцію.

За відомою кореляційною функцією можна знайти такі ймовірнісні характеристики:

середнє значення випадкового процесу.

;

середнє значення квадрата випадкового процесу.

;

дисперсію середньоквадратичне відхилення.