Крапка в системі двох площин проекцій p 1 і p 2

Рассмотрим построение проекций некоторой точки А, расположенной в первой четверти системы p1/p2 (рис. 2.3). Проведя из, А перпендикуляры (проецирующие лучи из бесконечно удаленных центров S1 и S2) к плоскостям проекций p1 и p2, получаем проекции точки А: горизонтальную проекцию А1, и фронтальную проекцию А2. Если спроецировать отрезки лучей АА1 из центра S2 и АА2 из центра S1, то получаем две… Читати ще >
Крапка в системі двох площин проекцій p 1 і p 2 (реферат, курсова, диплом, контрольна)
Построение проекций точки (и любого геометрического образа) в системе двух взаимно перпендикулярных плоскостей проекций осуществляется ортогональным проецированием на каждую плоскость.
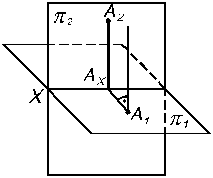
Рассмотрим построение проекций некоторой точки А, расположенной в первой четверти системы p1/p2 (рис. 2.3). Проведя из, А перпендикуляры (проецирующие лучи из бесконечно удаленных центров S1 и S2) к плоскостям проекций p1 и p2, получаем проекции точки А: горизонтальную проекцию А1, и фронтальную проекцию А2.
Если спроецировать отрезки лучей АА1 из центра S2 и АА2 из центра S1, то получаем две взаимно перпендикулярные прямые А2Ах и А1Ах, соответственно. Эти прямые принято называть линиями связи проекций.
Проверим, верна ли обратная задача.
Если даны проекции А1, А2 некоторой точки А, то определяют ли они положение точки в пространстве (рис. 2.4).
Решение:
- 1. Проведем из точки А1 перпендикуляр к плоскости p 1 (рис. 2.5).
- 2. Проведем из точки А2 перпендикуляр к плоскости p 2 (рис. 2.6).
- 3. Фигура АА1АхА2 имеет:

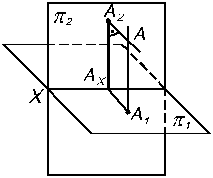
Следовательно, точка, А есть точка, принадлежащая двум пересекающимся перпендикулярам, лежащим в одной плоскости, и она единственная.
Таким образом, доказано, что две проекции определяют положение точки в пространстве.