Параметри прямої. 
Алгоритм побудови, параметричне дослідження та передача інформації на графічних моделях геометричних тіл. 
Програмний пакет Framemaker

Пряма лінія у просторі визначається чотирма параметрами, які зокрема можуть бути координатами точок перетину прямої з координатними площинами: (рис. 1.4). При звільненні всіх чотирьох параметрів прямої простір заповнюється чотирипараметричною множиною прямих і називається чотиривимірним лінійчастим простором.

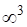
Рис. 1.4. Параметри прямої.

Зв’язуючи параметри лінійчастого простору, з нього можна вилучити такі підмножини прямих:

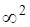
1. — комплекс прямих (рис. 1.5,а);

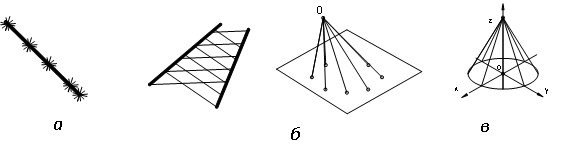
• 2. — конгруенція прямих, або її окремі випадки (двопараметричні в’язки прямих, або плоске поле прямих) (рис. 1.5,б);
• 3. — лінійчаста поверхня, або її окремий випадок — однопараметрична в’язка прямих (рис. 1.5,в).

На рис. 1.5 показано наочні приклади підмножин прямих у просторі.

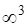
Рис. 1.5. Приклади підмножин прямих у просторі.

Форма і положення підмножини прямих, що вилучається з лінійчастого простору залежать від вигляду аналітичних залежностей між параметрами прямої. Кожна функціональна залежність між параметрами прямої зв’язує один параметр лінійчастого простору [3,4].

Параметри площини

Площина у просторі визначається трьома параметрами (рис. 1.6). Зокрема, у декартовій системі координат такими параметрами можуть бути відрізки, які площина відсікає на координатних осях. Якщо звільнити три параметри пло-щини, то простір заповнюється трипараметричною множиною площин (). При заданні функціональних залежностей (рівнянь) між параметрами площини, з простору вилучають-ся такі підмножини площин:

1. — двопараметрична в’язка площин (множина площин, що дотикаються до нерозгортної поверхні, або проходять через одну точку) (рис. 1.6,а).

Рис. 1.6. Площина у просторі.

2. — однопараметрична в’язка площин (множина площин, що дотикаються до розгортної поверхні, або проходять через одну пряму) (рис. 1.6,б).