Загальна характеристика методів рішення систем лінійних рівнянь

Релаксація лінійний рівняння Метод релаксації (по-російському: ослаблення) у його найпростішій формі полягає в тім, що на кожному кроці перетворюють у нуль максимальну по модулі нев’язання шляхом зміни значень відповідного компонента наближення. Процес закінчується, коли всі нев’язання останньої перетвореної системи будуть рівні 0 із заданою точністю. Питання про збіжність цього процесу… Читати ще >
Загальна характеристика методів рішення систем лінійних рівнянь (реферат, курсова, диплом, контрольна)
Способи вирішення систем лінійних рівнянь в основному розділяються на дві групи: 1) точні методи, що представляють собою кінцеві алгоритми для обчислення корінь системи (до таких методів ставляться: правило Крамера, метод Гаусса, метод головних елементів, метод квадратних корінь і ін.), і 2) ітераційні методи, що дозволяють одержувати корінь системи із заданою точністю, шляхом збіжних нескінченних процесів (до їхнього числа належать метод ітерацій, метод Зейделя, метод релаксації і ін.).
Внаслідок неминучих округлень результати навіть точних методів є наближеними, причому оцінка погрішностей корінь у загальному випадку скрутна. При використанні ітераційних процесів, поверх того, додається погрішність методу.
Однак ефективне застосування ітераційних методів істотно залежить від вибору початкового наближення й швидкості збіжності процесу.
Метод релаксації змінних систем лінійних рівнянь
П.З.:
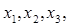
Дана система лінійних рівнянь, необхідно знайти та ін.
Нехай маємо наступну систему лінійних рівнянь:

(1).
Перетворимо цю систему в такий спосіб: перенесемо вільні члени ліворуч і розділимо перше рівняння на — б друге на — і т.д. Тоді одержимо систему, приготовлену до релаксації,
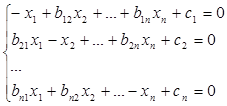
(2).
де.
и.

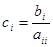
Нехай початкове наближення рішення системи (2). Підставляючи ці значення в систему (2), одержимо нев’язання.
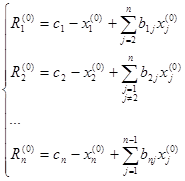
(3).
Якщо однієї з невідомих дати приріст, то відповідне нев’язання зменшиться на величину, а всі інші нев’язання збільшаться на величини. Таким чином, щоб звернути чергове нев’язання в 0, досить величині дати приріст.
і ми будемо мати:
и.
при.
релаксація лінійний рівняння Метод релаксації (по-російському: ослаблення) у його найпростішій формі полягає в тім, що на кожному кроці перетворюють у нуль максимальну по модулі нев’язання шляхом зміни значень відповідного компонента наближення. Процес закінчується, коли всі нев’язання останньої перетвореної системи будуть рівні 0 із заданою точністю. Питання про збіжність цього процесу ми залишаємо без розгляду .