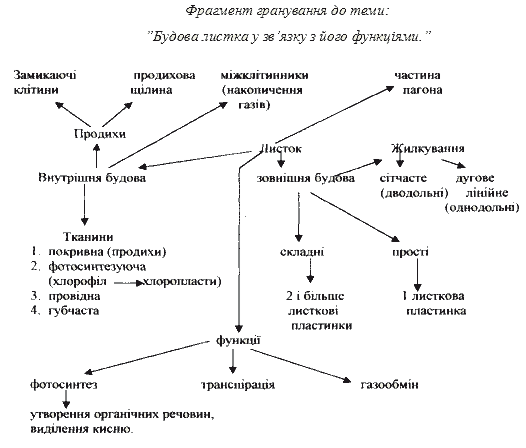
Розділ 3. Аналіз динаміки та стійкості урожайності сільськогосподарських культур

Під урожайністю розуміють середній вихід конкретної продукції з одиниці площі посіву (гектара, квадратного метра, дерева, куща тощо) даної культури (групи однорідних культур) або з одиниці площі сільськогосподарських угідь (як правило, в центнерах з гектара) [3].

Для виявлення тенденцій в зміні чисельності урожайності потрібно провести вирівнювання, тобто проаналізувати урожайність більш глибоко та всебічно.

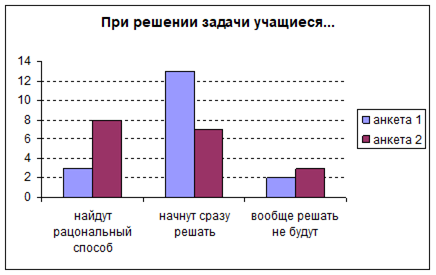
То ж проведемо розрахунки показників динаміки урожайності зернових культур в СВК «Шлях волі» в таблиці 3.1.

Таблиця 3.1 Розрахунок показників динаміки урожайності зернових в ООО «ПУСК».

У даній таблиці для аналізу були використані такі показники, як абсолютний приріст, темп зростання, темп приросту, абсолютне значення 1% приросту.

Абсолютний приріст показує на скільки одиниць збільшився (зменшився) рівень порівняно з базисним, тобто за цей або інший проміжок часу. Він розраховується як різниця між порівняльними роками:

А_баз = у_i — у₀, де (3.1).

— первинний рівень ряду динаміки;

— рівень ряду динаміки.

Якщо за базу порівняння приймається попередній рівень, то ланцюговий абсолютний приріст дорівнює:

А_лан. = у_i — у_{i-1 ,} де (3.2).

— рівень ряду динаміки;

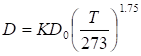
— попередній рівень ряду динаміки.

Темп росту показує в скільки разів збільшився рівень, порівняно з базисним, а у випадку зменшення — яку частину базисного рівня складає порівняний рівень:

Тр_баз = (3.3).

Якщо за базу порівняння приймається попередній рівень, то ланцюговий темп росту дорівнює:

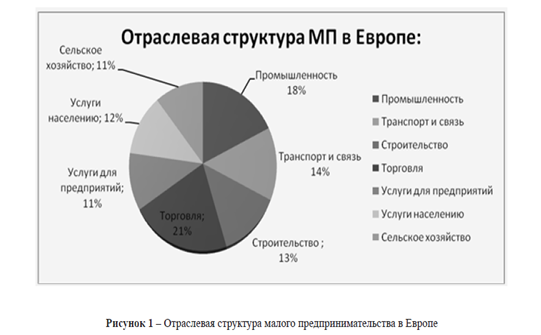
Тр_лан. = (3.4).

Темп приросту показує на скільки відсотків збільшився (зменшився) рівень, порівняно з базисним, прийнятим за 100%.

Тпр_баз = Тр_баз-100% (3.5).

Тпр_лан = Тр_лан.-100% (3.6).

Абсолютне значення 1% приросту розраховується шляхом ділення абсолютного приросту на відповідний темп приросту, виражений в %.

= А_i/Тпр_i (3.7).

Також за даними, розрахованими в таблиці 3.1 можна визначити середні показники:

1. Середнє значення урожайності, яке розраховується за формулою середньої арифметичної простої.

= у/n, де (3.8).

у — сума значень рівня ряду динаміки;

n — число рівнів ряду динаміки.

У= 216,3/7 = 30,9 ц/га.

2. Середній абсолютний приріст показує як швидко змінився кінцевий рівень ряду динаміки відносно початкового, він розраховується за формулою:

= А_лан/n-1, де (3.9).

А_лан — сума абсолютних приростів, А = -3,8/6 = -0,63 ц/га.

3. Середній темп росту характеризує середню швидкість зміни економічного явища або процесу і визначається за формулою:

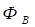
Тр.=, де (3.10).

Тр — середній коефіцієнт (темп) росту;

уn — останній рівень ряду динаміки;

у0 — початковий рівень ряду динаміки;

n — число рівнів ряду динаміки.

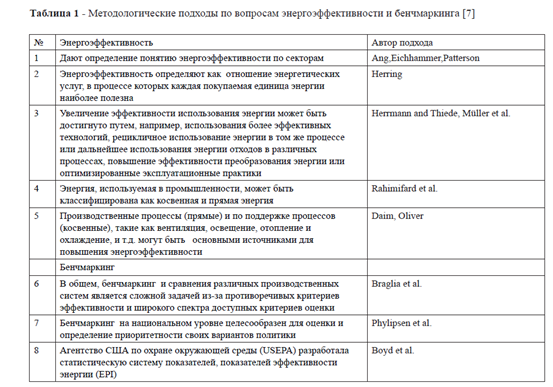
Тр = = 0,980 або 98,0%.

4. Середній темп приросту відрізняється від середнього темпу росту на 100% та визначається:

Т_пр = Тр — 100% (3.11).

Т_пр =98,0 — 100 = ?2%.

Аналізуючи розрахунки показників динаміки урожайності, можна зробити висновки, що в середньому щорічно урожайність зернових культур зменшувалася на 0,63 ц/га, середній темп приросту, який дорівнює -2 означає те, що щорічно урожайність зменшувалася на 2%.

Ряд динаміки — це ряд числових характеристик, які характеризують зміни показників суспільного явища в часі.

Ряд динаміки складається з рівня числового значення ознаки, що вивчається, і часу, до якого відноситься дана ознака.

Одним з найважливіших напрямів аналізу рядів динаміки є вивчення особливостей розвитку явища за окремі періоди часу. Для виявлення специфіки розвитку явищ, що вивчаються, за окремі періоди часу визначають абсолютні і відносні показники ряду динаміки:

При визначенні цих показників використовують два методи: ланцюговий і базисний.

У даному курсовому проекті динамічний ряд будується на основі показника урожайності зернових.

Виявимо тенденцію в зміні урожайності зернових та проведемо вирівнювання ряду динаміки (таблиця 3.2).

Роки.	Урожайність, ц/га.	Вирівнювання по рівнянню прямої лінії.	Вирівнювання по параболі II-го порядку.
=.	=.
	33,5.	— 5.	— 167,5.		33,45.		837,5.	36,03.
	39,4.	— 3.	— 118,2.		32,43.		354,6.	32,29.
	25,2.	— 1.	— 25,2.		31,41.		25,2.	29,91.
	27,6.				30,9.			29,23.
	28,1.		28,1.		30,39.		28,1.	28,89.
	32,8.		98,4.		29,37.		295,2.	29,23.
	29,7.		148,5.		28,35.		742,5.	30,93.
Всього.	216,3.		— 35,9.		216,3.		2283,1.	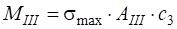216,5.

Вирівнювання руху динаміки способом найменших квадратів дозволяє враховувати всі рівні динаміки та краще абстрагуватись від випадкових коливань рівнів. Цей метод передбачає вирівнювання за рівнянням прямої лінії:

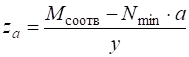
=, де (3.12).

— вирівнювання значення ряду по роках.

a0, a1 — параметри рівняння,.

t — порядковий номер .

Для знаходження параметрів a0 та a1 складемо систему двох нормальних рівнянь:

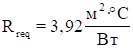
(3.13).

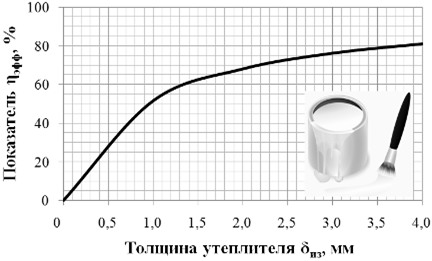
Так як, то знайдемо з першого рівняння системи (3.13).

=.

= 30,9.

Тепер знайдемо з другого рівняння системи (3.13).

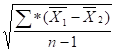
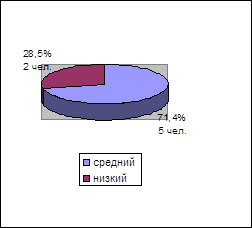
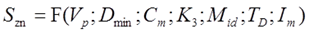
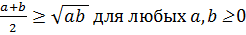
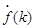
Рівняння прямої матиме вигляд:

=30,9 — 0,51t.

Існує ще один спосіб вирівнювання динамічного ряду — це вирівнювання по параболі ІІ порядку. Для цього треба розрахувати систему рівнянь:

(3.14).

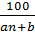
Так як і, тому система буде мати вигляд:

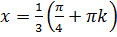
(3.15).

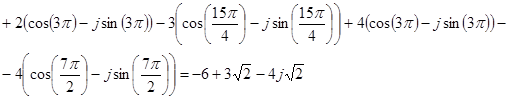
Параметр а2 знайдемо з системи рівнянь:

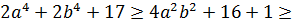
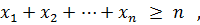
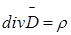
Тоді буде дорівнювати:

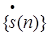
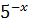
Рівняння параболи має такий вигляд:

= 29б23 — 0,51+ 0,17.

Результати розрахунку приведені в таблиці 3.2.

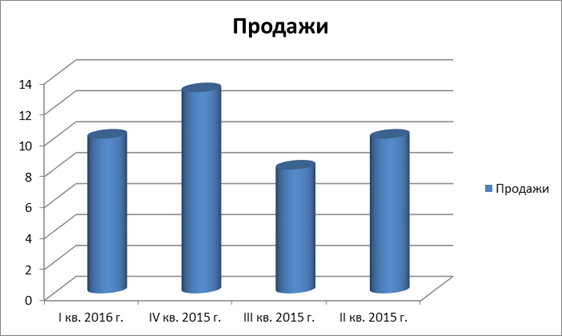
Побудуємо графік аналітичного вирівнювання урожайності зернових:

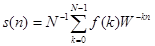
Рис. 3.1 Аналітичне вирівнювання урожайності зернових в ООО «ПУСК»

Аналізуючи отриманий графік, можна зробити наступний висновок, що фактична урожайність збільшилася в 2002р., але в 2003р. знизилася, з 2004 по 2006р урожайність зростала, а в 2007 році вона знову знизилась. Урожайність, вирівняна по прямій має тенденцію до зниження; по параболі урожайність в 2001 — 2005 спадає, а з 2006 р. має тенденцію до підвищення.

Проаналізуємо стійкість динамічного ряду за допомогою коефіцієнтів детермінації, кореляції та стійкості в таблиці 3.3.

Таблиця 3.3 Аналіз стійкості урожайності зернових культур в ООО «ПУСК».