Визначення моментів інерції твердих тіл з допомогою трифілярного підвісу

Мета .

Прилади .

Теоретичні відомості

Момент інерції - це фізична величина, що є мірою інертності тіл при обертовому русі. Чисельно вона дорівнює сумі добутків мас матеріальних точок, на які подумки розбивають тіло, на квадрати їх віддалей від осі обертання:

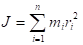
У випадку однорідного тіла правильної форми сума замінюється інтегруванням. На практиці часто необхідні значення моментів інерції твердих тіл неоднорідних або довільної (неправильної) форми. У таких випадках моменти інерції визначають експериментально. Одним з методів визначення моментів інерції є метод трифілярного підвісу. Трифілярний підвіс являє собою круглу платформу, що підвішена на трьох симетрично розташованих нитках, прикріплених до країв цієї платформи. Зверху ці нитки також симетрично прикріплені до диска меншого діаметра, ніж діаметр платформи. Платформа може здійснювати крутильні коливання навколо (Рис. 1.) вертикальної осі, що перпендикулярна до її площини та проходить через її середину. Центр мас платформи при цьому переміщується вздовж осі обертання. Період коливань визначається величиною моменту інерції платформи. Він буде іншим, якщо платформу навантажити яким-небудь тілом. Це й використовується в даній роботі.

Якщо платформа масою m, обертаючись в одному напрямку, піднялась на висоту h, то вона набуде приросту потенціальної енергії.

W = mgh,.

інерція прискорення твердий підвіс де g — прискорення вільного падіння.

Обертаючись в другому напрямку, платформа прийде в положення рівноваги з кінетичною енергією:

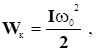
де І - момент інерції платформи;

0 — кутова швидкість платформи в момент досягнення нею положення рівноваги.

Знехтувавши роботою сил тертя, на основі закону збереження механічної енергії, можемо записати:

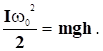
(1).

Вважаючи, що платформа здійснює гармонічні коливання, можемо записати залежність кутового зміщення платформи від часу в вигляді:

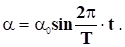
де — кутове зміщення платформи;

0 — амплітуда зміщення;

Т — період коливань;

t — поточний час.

Кутова швидкість визначається як перша похідна від кута за часом, тобто:

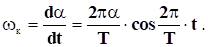
В моменти проходження через положення рівноваги (t = 0, 0.5Т; 1.5Т і т.д.) абсолютне значення її буде:

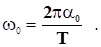
Підставивши значення 0 в рівняння (1), одержимо:

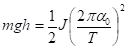
(2).

Якщо l — довжина ниток підвісу, R — радіус платформи, r — радіус верхнього диска, то з рис. 1. видно, що.

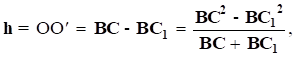
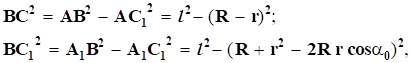
тому.

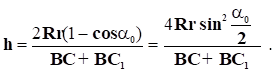
При малих значеннях кута відхилення 0 синус цього кута можна замінити значенням самого кута в радіанах, а знаменник вважати рівним 2l. Врахувавши це, одержимо:

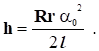
Підставивши значення h у рівняння (2), маємо:

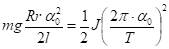
(3).

звідки одержуємо остаточно:

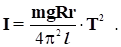
(4).

За формулою (4) можна визначити момент інерції і самої платформи і тіла, що покладене на неї, так як всі величини, правої частини формули можуть бути безпосередньо виміряні.

Трифілярний підвіс дає можливість також перевірити теорему Штейнера:

І = І0 + ma2. (5).

Момент інерції тіла відносно якої-небудь осі дорівнює сумі моменту його інерції відносно паралельної осі, яка проходить через центр мас, та добутку маси тіла на квадрат віддалі між осями.

Для перевірки теореми Штейнера необхідно мати два абсолютно однакових тіла. Спочатку визначають момент інерції одного з них, а потім обидва тіла розміщують симетрично на платформі і визначають їх момент інерції при такому розташуванні. Половина цього значення і буде давати момент інерції одного тіла, що знаходиться на фіксованій віддалі від осі обертання. Знаючи віддаль, масу тіла та момент інерції його відносно центральної осі, можна вирахувати момент інерції цього ж тіла за теоремою Штейнера. Порівняння одержаних значень моментів інерції і буде перевіркою теореми.

Порядок виконання роботи

1. Повернути нижню платформу на кут 8−100, надавши їй обертовий імпульс для початку крутильних коливань. Секундоміром виміряти час 25−30 повних коливань підвісу та визначити період коливань за формулою:

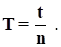
(6).

• 2. У центрі платформи розташувати досліджуване тіло m1 та визначити період коливань системи T1.
• 3. На платформі симетрично відносно центру розмістити два тіла масою m1 і визначити період коливань системи T2.

Штангенциркулем заміряти радіус досліджуваного диска r1, та віддаль a між центрами платформи і зміщеного диска. Дані всіх вимірювань занести в таблицю:

Обробка результатів експерименту та їх аналіз За формулою (4) вирахувати момент інерції I0 платформи. У цьому випадку m=m0, T=T0.

За формулою (4) вирахувати момент інерції I0 платформи, навантаженої диском m1. У даному разі m=m0+m1; T=T1.

Із співвідношення IC=I0+Iд знайти момент інерції диска відносно центральної осі Iд.

За теоретичною формулою Iд= 0.5m1r12 знайти момент інерції цього ж диска. Результат співставити з експериментальним.

За формулою (4) вирахувати момент інерції I2 платформи, навантаженої двома симетрично розташованими дисками m1.

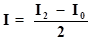
За формулою знайти момент інерції диска відносно осі, зміщеної на O від центра мас.

За формулою (5) вирахувати момент інерції зміщеного диска згідно з теоремою Штейнера. Результат співставити з експериментом.

Знайти відносну та абсолютну похибки одного з експериментів.

Визначаємо періоди повних обертань:

А) Визначаємо період коливань платформи:

.

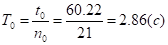
Б) Визначаємо період коливань платформи із вантажем, розташованим по центру:

.

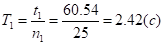
В) Визначимо період коливань платформи з двома на ній розташованими вантажами:

.

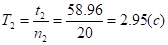
Заповнимо таблицю:

Підрахуємо момент інерції платформи (I0) без вантажів:

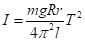
де та .

.

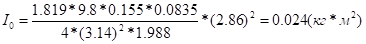
Підрахуємо момент інерції платформи з вантажем, масою m1 по середині:

де та .

.

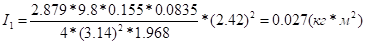
Підрахуємо момент інерції платформи з вантажами, масами m1, розташованих симетрично:

де та .

.

Знайдемо момент інерції диска відносно центральної осі :

.

Знайдемо теоретично момент інерції диска відносно центральної осі :

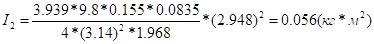
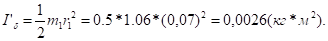
Бачимо, що результат майже однаковий (похибка — 7,8%, що пояснюється неточністю практичних вимірювань).

Знайдемо момент інерції диска відносно осі, зміщеної на Овід центра мас:

.

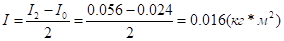
Підрахуємо за теоремою Штейнера момент інерції зміщеного диску:

.

А цей результат становить відхилення у 2,6% практичного.

Підрахуємо похибку практичного вимірювання моменту інерції:

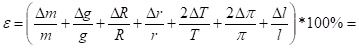
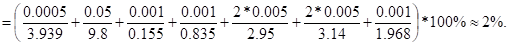
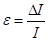
звідки .

Висновок: Отож, на сонові цієї лабораторної роботи ми впевнились у вірності вимірювання моменту інерції твердих тіл за допомогою трифілярного підвісу. Вірність досліду нам довів теоретичний шлях вимірювання моменту інерції за використанням теореми Штейнера.