Аналіз предметної області

Аналіз інформаційного забезпечення

Лінійна алгебра — частина алгебри, що вивчає векторні (лінійні) простору і їх підпростори, лінійні відображення (оператори), лінійні, білінійні, і квадратичні функції на векторних просторах.

Лінійна алгебра, математичні методи — розділ обчислювальної математики, присвячений математичному опису та дослідженню процесів чисельного рішення задач лінійної алгебри.

Серед задач лінійної алгебри найбільше значення мають дві: рішення системи лінійних алгебраїчних рівнянь визначення власних значень і власних векторів матриці. Інші часто зустрічаються задачі: звернення матриці, обчислення визначника і т.д.

Будь-який чисельний метод лінійної алгебри можна розглядати як деяку послідовність виконання арифметичних операцій над елементами вхідних даних. Якщо за будь-яких вхідних даних чисельний метод дозволяє знайти рішення завдання за кінцеве число арифметичних операцій, то такий метод називається прямим. В протилежному випадку чисельний метод називається ітераційним. Прямі методи — Це такі, як метод Гауса, метод облямівки, метод поповнення, метод спряжених градієнтів та ін. Ітераційні методи — це метод простої ітерації, метод обертань, метод змінних напрямків, метод релаксації і ін. Тут будуть розглядатися матричний метод, метод Гауса і метод Крамера.

Рівняння виду.

(1).

називається лінійним рівнянням з n невідомими:. Слово лінійне означає, що рівняння 1-го степеня.

Розв’язком такого рівняння буде такий упорядкований набір чисел, який перетворює наше рівняння в числову тотожність.

Рівняння виду (1) можна використати для побудови системи рівнянь:

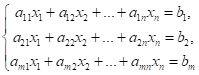
(2).

Система (2) називається системою m лінійних рівнянь з n невідомими.

Якщо кількість рівнянь даної системи (m) не дорівнює кількості невідомих (n), то таку систему називають прямокутною системою.

Якщо m=n, то система називається квадратною.

Розв’язком системи (2) будемо називати такий набір чисел, який задовольняє кожне рівняння системи (2). Це буде перетин множин розв’язків кожного рівняння даної системи.

Якщо система (2) має принаймні один розв’язок, то така система називається сумісною.

Якщо ж система (2) зовсім не має розв’язків, то система називається несумісною.

Якщо система (2) має точно один розв’язок, то така система називається визначеною. Якщо система (2) має більше, ніж один розв’язок, то вона називається невизначеною.

програма вирішування лінійний рівняння Класифікація систем Крім того в системі (2) всі вільні члени можуть бути рівні 0. Тоді система має такий вид:

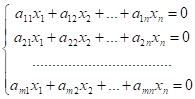
(3).

Системи виду (3) називається однорідними.

Однорідна система завжди сумісна, тому що вона завжди має принаймні один розв’язок — нульовий.

Нехай задана система лінійних рівнянь з невідомими коефіцієнтами при яких є елементами матриці А, а вільними членами є числа.

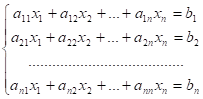
(4).

Якщо визначник системи (4), тобто визначник, що складається з коефіцієнтів при невідомих.

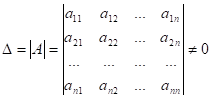
(5).

то система (4) має єдиний розв’язок.

Системи лінійних алгебраїчних рівнянь відіграють важливу роль у математиці, оскільки до них зводиться велика кількість задач лінійної алгебри, теорії диференціальних рівнянь, математичної фізики тощо, та областей фізики й техніки, де застосовуються ці математичні теорії.