Введення в теорію перколяції

Теорія перколяції має справу з дуже простими моделями невпорядкованих систем. В роботі буде пояснено основні поняття і результати перколяційних досліджень, використаних в найпростіших перколяційних проблемах: так званих випадкових ділянках перколяції в періодичних двовимірних ґратках.

На рис. 1 зображено серію кінцевих (50×50) квадратних ґраток, ділянки яких (зображені квадратами на рис. 1) можуть знаходитись в двох станах, які мають назви «зайнятий» (чорні квадрати) і «вільний» (білі квадрати). Кожен випадковий квадрат може бути зайнятим (не залежить від стану інших) з імовірністю p або вільним з імовірністю 1-p. Група зайнятих квадратів, зв’язаних найменшими відстанями між собою має назву перколяційний кластер. Якщо p є малим (наприклад, p=0,1), то більш зайняті місця є ізольованими від маленьких кластерів (рис. 1(а)). Якщо p збільшується, більшає і величина кластерів, починає з’являтись комплекс неправильної форми (рис. 1 (б)-(д)) і для деякого значення p кластер зростається в єдине ціле (рис. 1 (д),(ф)). В обмеженні нескінченної граки таке значення p називають перколяційним порогом, при якому неперервний кластер зумовлює провідність з кінцевою імовірністю (наприклад, p_c на квадратній ґратці рівна 0,592 745±0,2 (за результатами числового моделювання Зіффа і Саповала в 1986р)). [3].

Поріг перколяції — це точка, що знаходиться між непровідним (неперервного кластера немає) і провідним станами (неперервний кластер існує), при якій властивості перколяційної системи несподівано змінюються при підвищенн p (перколяційний фазовий перехід, який є фазовим переходом другого роду). При p>p_c неперервний кластер починає приєднувати до себе менші кластери (на рис. 2 зображено залежність густини неперервного кластера від р).

Вивчення властивостей перколяційних кластерних форм є принциповою частиною перколяційного вчення. Зокрема, вивчення розподілу розмірів кластерів і структури дуже великих кластерів поблизу порогу протікання електричного струму — явище, яке останнім часом вивчалось найбільше. Але геометричний розподіл є також дуже важливим, оскільки, головний напрям перколяційної теорії є основаним на можливості зіставлення геометричних властивостей з транспортними (такими, як електропровідність).

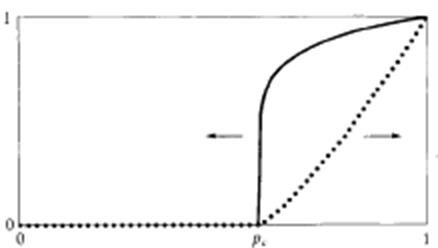
Рис. 2. Залежність густини (суцільна лінія) і провідності (точкова лінія) неперервного кластера від р.

Для прикладу, уявімо, що на рис. 1 забарвлені квадратики відповідають провідним речовинам, а світлі - діелектрикам і, що дві провідні площини є електрично поєднані тільки тоді, коли контактують між собою. Тоді електричний стум може протікати від однієї сторони зразка до іншої лише в випадку проходження кластера повністю через гратку. Якщо діелектричні речовини знаходяться між кожною парою електрично зв’язаних площин, то вони утворюють резисторну мережу. Вивчення випадкових резисторних мереж стало порівняно незалежним і виросло в окрему галузь перколяційної теорії, що дуже швидко розвивається і вже знайшла власне застосування в таких важливих питаннях, як, наприклад, вивчення оптичних властивостей композитних матеріалів. [6].

В цій роботі я спробую проілюструвати можливості перколяційної ідеї на прикладі її застосування в вивченні тонких металевих плівок на напівпровідниковій чи діелектричній підкладках (скло, слюда, сапфір, нітрид кремнію та ін.). Ріст таких плівок, які зазвичай отримуються шляхом вакуумного випаровування, проходить так: перші металеві зерна утворюють невеликі острівки, що формуються на підкладці і розростаються на ній, згодом утворюючи металеву мережу (по аналогії з нескінченним перколяційних кластером, зображеним на рис. 1(с)), яка простягається на весь зразок і змушує поводитись його як метал (якщо ми вивчаємо його провідність). Властивості напівнеперервних металевих плівок (тобто, таких плівок, які є недалекими від утворення неперервного кластера) є основною метою перколяційного вчення в тонких металевих плівках. [1].

Аналіз рис. 3 показує, що металеві зерна випадковим чином розподілені на підкладці і не утворюють періодичну гратку, тобто модель випадкового розподілу є більш вигідною для опису морфології плівки, аніж моделі, в основі яких лежить твердження про впорядкованість ґратки. 7] До недавнього часу, всі дослідники перколяційної теорії вірили в достовірність так званої гіпотези універсальності (наприклад, Стенлі 1971, Уілсон 1979), яка в даному випадку говорила про те, що критичні властивості не залежать від того, чи заповнюються вільні місця чи ні. Але універсальність дає можливості перенесення результатів отриманих для технічно більш вигідної моделі випадкового розподілу.

Вивчення вище згаданої моделі (модель швейцарського сиру) показало, що явище провідності зумовлене не лише транспортними властивостями перколяційних кластерів.

Також, важливим є питання про те, що значить імовірність протікання (концентрація зайнятих вузлів) p при випадковому розподілі тонкої металевої плівки (рис. 3). Порівняння малюнків 3 та 1 дає можливість вважати, що p — відсоткова доля поверхні, покрита металом.

Рис. 3. Плівки Au товщиною 4 нм на вуглецевій підкладці. Металеві ділянки зафарбовано чорним. (P = 0,48)

Покриття поверхні може бути визначеним шляхом електронної мікроскопії, але плівка повинна бути виготовлена на спеціальній підкладці (прозорій для електронів) і, зазвичай, вона повинна бути видалена з вакуумної камери. Таким чином, дослідження проведені Палевським та іншими (1984) є дуже важливим: вони виявили, що товщина t плівки, визначена кварц-мікроваговим методом, пропорційна покриттю поверхні р в широкому діапазоні товщини поблизу протікання, звідси, (t-t_c) ~ (p-p_c) де t_c — товщина, що відповідає p_c. Так як товщина може бути виміряна на місці (без переривання вакууму) в процесі напилення, то це дає можливість вивчати нестабільні напівнеперервні структури. 3].