Розділ 2. Застосування двоїстості в задачах нелінійного програмування

Теорія двоїстості знайшла своє практичне застосування і в задачах нелінійного програмування. Розглянемо тепер задачу нелінійного програмування у вигляді:

(2.1).

при обмеженнях:

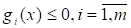
.(2.2).

Ввівши функцію Лагранджа.

.

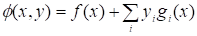
можна записати цю задачу в еквівалентному вигляді:

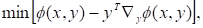
(2.3).

при обмеженнях:

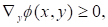
.(2.4).

За аналогією з лінійним програмуванням назвемо таку задачу:

(2.5).

при обмеженнях:

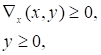
(2.6).

двоїстою до задачі (2.3) — (2.4).

Має місце теорема, аналогічна теоремі двоїстості ЛП, вперше доведена П. Вульфом.

Теорема 2.1. Нехай функції.

, ,.

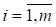
опуклі та диференційовані в і виконуються умови регулярності. Якщо пряма задача (2.1) — (2.2) має розв’язок, то в двоїстій задачі (2.6) існує такий вектор, який є її оптимальним розв’язком і при цьому екстремуми пари двоїстих задач рівні між собою.

Для ілюстрації цієї теореми розглянемо задачу квадратичного програмування:

(2.7).

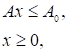
(2.8).

де С — симетрична, від'ємно визначена матриця. Перетворимо (2.7) — (2.8) в еквівалентну задачу мінімізації і побудуємо функцію Лагранджа:

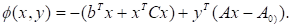
(2.9).

Вихідну задачу можна записати у такому вигляді:

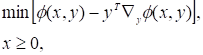
(2.10).

.(2.11).

Неважко показати, що задача (2.10) — (2.11) еквівалентна задачі (2,7) — (2,8).

За аналогією з лінійним програмуванням запишемо двоїсту задачу для задачі квадратичного програмування:

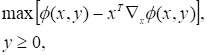
(2.12).

при обмеженнях:

(2.13).

Підставляючи вираз для із (2.9) в (2.12) і (2.13), дістанемо таку форму запису двоїстої задачі:

(2.14).

.(2.15).

Оптимальні розв’язки та зв’язані між собою співвідношеннями:

(2.16).

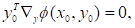
(2.17).

Використовуючи вираз (2.9) і підставляючи його в (2.16) та (2.17), знаходимо відповідно:

• (2.18)
• (2.19)

Покажемо, що задачі (2.7) — (2.8) і (2.14) — (2.15) справді є двоїстими і виконується твердження теореми про те, що.

.(2.20).

Оскільки звя’зані між собою співвідношеннями (2.18) та (2.19), то маємо Або Таким чином, встановлено справедливість відношення (2.20) і теореми (2.1).