Вирішення типових завдань зі статистики

Задача 1

Произведено 10% обследование промышленных предприятий региона, в результате которого при механическом способе отбора получены данные о численности работников 80 промышленных предприятий (чел).

1550 1500 3000 1500 1500 2400 2600 1700 1000 15 000 2200 2150 3000 2450 2700 1860 1760 2650 2450 2100 3000 940 1150 2900 550 2300 2100 2950 2000 1600 2550 1680 2500 1400 1550 1300 1660 2200 1500 2000 2050 1100 2800 2500 3000 1330 2350 1550 2600 2600 2700 3060 1900 2550 2900 3100 2300 2320 2150 2750 2000 2900 2100 2350 1900 1105 2800 3100 2440 1700 830 2472 3800 1500 2500 2900 3490 2475 3100 900.

По этим данным:

постройте интервальный ряд распределения;

изобразите полученный ряд графически в виде гистограммы и полигона распределения;

определите: среднюю численность работников предприятия, среднее квадратическое отклонение; коэффициент вариации, моду и медиану;

с вероятностью 0,993 определите предельную ошибку выборочной средней и возможные границы, в которых ожидается средняя численность работников для всех предприятий региона;

с вероятностью 0,996 установите предельную ошибку выборочной доли и границы удельного веса предприятий с численностью работников более 1660 человек.

Сделать выводы.

Решение

Находим xmin =550 чел. и xmax =3800 чел.

Размах вариации R= xmax-xmin=3800−550=3250.

По формуле Стерджесса определяем ширину интервала:

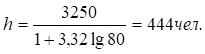
Устанавливаем полную шкалу интервалов:

а₁ = 550 — 444/2= 328,.

в₁ = a₁ + h = 328 + 444 = 772,.

b₂ = a₂ + h = 772 + 444 = 1216 и т. д.

Записываем полученные интервалы в табл. 4 и производим группировку данных по полученным интервалам.

Таблица 4. Распределение заводов по численности работающих.

Графически интервальный ряд распределения предприятий изображается гистограммой (рис.1) и полигоном (рис.2):

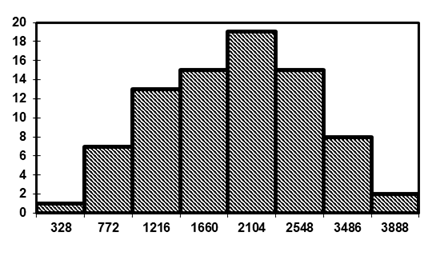
Рис. 1. Гистограмма распределения предприятий по численности работающих

Определим среднюю численность работников, среднее квадратическое отклонение и коэффициент вариации. Для этого составим расчетную табл. 5.

Воспользовавшись суммарным итогом графы 4, рассчитаем среднюю численность работников предприятий:

Дисперсию изучаемого распределения вычислим на основании итога, полученного в графе 6:

Таблица 5. Расчет среднего и среднего квадратического отклонения.

Группы предприятий.	Число заводов, mi	Центры интервалов, xi	ximi
328 — 772.				— 1615.05.	2 608 386.5.
772 — 1216.				— 1171.05.	9 599 506.7.
1216 — 1660.				— 727.05.	6 871 822.1.
1660 — 2104.				— 283.05.	1 201 759.6.
2104 — 2548.				160.95.	4 921 193.1.
2548 — 2992.				604.95.	5 489 467.6.
2992 — 3436.				1048.95.	8 802 368.8.
3436 — 3880.				1492.95.	4 457 799.4.
Итого:		;		;	39 523 303.8.

Тогда среднее квадратическое отклонение:

= 702,88 чел.=703 чел.

Коэффициент вариации:

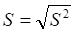
Средняя численность работников промышленных предприятий региона составляет 2165 человек. Среднее квадратическое отклонение описывает абсолютный разброс значений показателя X и в данном случае составляет 703 чел. Коэффициент вариации характеризует относительный разброс признака вокруг среднего значения и составляет 32.46%.

Определим моду по таблице 5. Модальный интервал — это тот, которому соответствует наибольшая частота (19 заводов). Следовательно, модальный интервал — это интервал с численность работающих от 2104 до 2548 человек. Для интервального ряда моду определим по формуле:

.

где х₀ — нижняя граница модального интервала, то есть 2104 чел.;

h — величина модального интервала (444 чел.);

m_Мо — частота модального интервала (19);

m_Мо-1 — частота интервала, предшествующего модальному (15);

m_Мо+1 — частота интервала, следующего за модальным (15).

Найдем медиану, то есть значение признака, приходящееся на середину ранжированной совокупности. Определим ее по формуле:

.

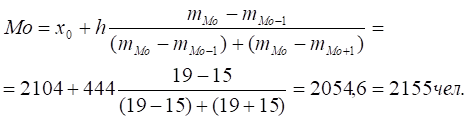
где х₀ — нижняя граница медианного интервала 2104 чел.);

h— величина медианного интервала (444 чел.);

m_Ме — частота медианного интервала (19);

S_Мe-1 — накопленная частота интервала, предшествующего медианному (36).

Для установления медианного интервала необходимо определить накопленную частоту каждого последующего интервала до тех пор, пока она не превысит половины суммы накопленных частот (в нашем случае 40 заводов).

Медианным является интервал с границами от 2104 до 2548 чел. (табл. 4).

Таким образом, мода равна 2155 человек, медиана — 2011 человек.

4. Определим общую численность промышленных предприятий (объем генеральной совокупности). Так как произведено 10% выборочное обследование и объем выборки составляет 80 предприятий, то N = 800.

Определим среднюю ошибку выборки для выборочной средней:

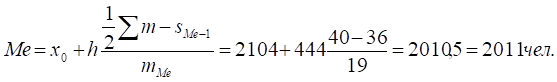
Т. е. средняя ошибка выборочной средней составляет 74,55 чел.

Определим коэффициент t для заданной доверительной вероятности 0.993. Из таблицы распределения нормального закона (прил.1) получаем.

t = 2,7.

Найдем предельную ошибку выборки чел.

Тогда доверительный интервал для ожидаемой средней численности работников промышленных предприятий региона определяется неравенством:

2165,5 — 201,3 < < 2165,5 + 201,3.

.

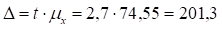
т. е. истинное значение генеральной средней находится в интервале от 1964 чел. до 2367 чел.

5. Определим выборочную долю предприятий, имеющих численность более 1600 человек. Суммируя численности предприятий в группах из таблицы 2, получим m = 59. Выборочная доля равна.

w = m / n = 59/80 = 0,74.

Определим среднюю ошибку выборки для выборочной доли:

т. е. средняя ошибка выборочной доли составляет 0,047.

Определим коэффициент t для заданной доверительной вероятности 0,996 из приложения 1. Из таблицы распределения нормального закона получаем t = 2,9.

Вычислим предельную ошибку выборки:

Тогда доверительный интервал для ожидаемой доли предприятий с численностью работников более 1660 чел. определяется неравенством:

0,74 — 0,14 < р < 0,74 + 0,14,.

0,6 < р < 0,88.

Таким образом, ожидаемая доля предприятий с численностью работников более 1600 человек находится в пределах от 0,6 до 0,88 или от 60% до 88%.

Задача 2

Имеется следующая информация о потреблении населением электроэнергии (млрд. кВт. Ч). Цифры условные:

2006 г. — 111, 2007 г. — 115, 2008 г. — 120, 2009 г. — 125, 2010 г. — 120, 2011 г. — 130.

Для анализа потребления электроэнергии определите:

показатели рядов динамики (цепные и базисные). Полученные результаты представьте в виде таблицы;

среднегодовое потребление электроэнергии;

среднегодовой темп роста и прироста потребления электроэнергии;

провести сглаживание ряда динамики;

сделайте выводы.

Решение

Расчетные показатели ряда динамики приведем в табл. 6:

Таблица 6. Анализ потребления населением электроэнергии.

Среднегодовой прирост потребления электроэнергии определим по формуле:

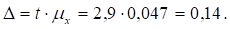
среднегодовой темп роста:

Средний уровень ряда:

Из анализа абсолютных приростов и темпов роста видно, что по сравнению 2006 годом, происходило увеличение потребления электроэнергии, за исключением 2010 года. Цепные абсолютные приросты показывают, что увеличение потребления происходило незначительно.

Ежегодное потребления электроэнергии увеличивалось на 3,8 млрд. кВт. ч., что составляет 3,2%. Среднее потребление электроэнергии за год составило 144,2 млрд. кВт. Ч.

Сглаживание ряда динамики проведем по формуле:

.

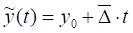
Получим: .

По двум точкам проводим прямую на графике.

Построим график потребления электроэнергии.

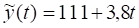
Рис. 3. Потребление электроэнергии

Задача 3

Имеется информация о размерах вкладов на счетах физических лиц, тыс. руб.:

на 1.01.11 — 4,0, на 1.02.11 — 5,5, на 1.03.11 — 6,5, на 1.04.11 — 8,0.

Определите средний размер вкладов за первый квартал.

Решение

Так как по условию задачи имеем моментный ряд, то средний уровень ряда определим по средней хронологической:

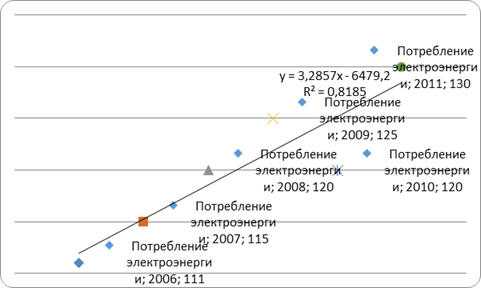
Таким образом, средний размер вкладов за первый квартал составил 6 тыс. руб.

Задача 4

Имеется информация о реализации продуктов на рынке (табл.7).

Определите:

индивидуальные и общий индексы цен;

индивидуальные и общий индексы физического объема;

общий индекс товарооборота в фактических ценах;

сумму экономического эффекта, полученную в отчетном периоде от изменения цен.

Таблица 7. Информация о продаже товаров на рынке.

Решение

1. Определим индивидуальный индекс цен для каждого продукта по

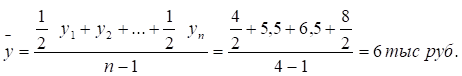
А: ip = 60/50 = 1,2 (120%);

Б: ip = 95/80 = 1,188 (118%);

В: ip = 42/30 = 1,40 (140%).

Цена на продукт, А в отчетном периоде по сравнению с базисным возросла на 20%, что составляет 10 рублей, на товар Б — на 18% или на 15 рублей, на В — на 40% или на 12 рублей.

Найдем общий индекс цен:

.

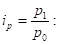
или 127,6%.

Найдем сумму экономического эффекта от изменения цен на продукты.

Цена отчетного периода по сравнению с базисным увеличилась на 27,6%, что составляет 2075 рублей, т. е. население из-за повышения цен переплатило за одно и то же количество продуктов 2075 рублей.

2. Подсчитаем индивидуальные индексы физического объема:

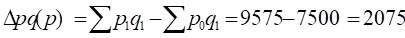
А: = 50/52 = 0,9615 или 96,15%;

Б: = 25/15 = 1,67 или 167,0%;

В: = 100/65 = 1,54 или 154,0%.

Объем продажи товара, А в текущем периоде по сравнению с базисным уменьшился на 100−96,15=3,85% или на 2 т, товара Б и В увеличился соответственно на 67% и 54% или на 10 и 35 т.

Определим общий индекс физического объема.

.

или 130,4%.

Найдем сумму экономического эффекта от изменения объема продаж:

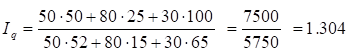
Объем продаж в отчетном периоде по сравнению с базисным увеличился на 30,4%, что составляет 1750 рублей.

Подсчитаем индекс товарооборота в фактических ценах:

.

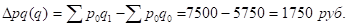
Сумма товарооборота отчетного и базисного периода подсчитана при исчислении общих индексов цен и физического объема:

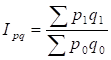
или 166%.

Общий объем товарооборота в фактических ценах увеличился в отчетном периоде по сравнению с базисным на 66%, что в абсолютном выражении составляет:

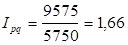
Правильность расчетов проверяется при помощи формулы взаимосвязи индексов:

Задача 5

В отчетном периоде по сравнению с базисным товарооборот увеличился на 30%, цены возросли на 4%. Найти изменение физического объема.

Решение

Из условия задачи определяем индексы.

Индекс товарооборота I_pq=1,3, индекс цен I_p=1,04.

Используя взаимосвязь индексов.

.

получим:

.

Таким образом, в отчетном периоде по сравнению с базисным, физический объем увеличился на 25%.

Задача 6

На основании данных обследования группы предприятий исследовать на основе линейной регрессионной модели зависимость прибыли от реализации продукции Y от среднегодовой численности промышленно-производственного персонала X (табл. 8).

Решение

Построим поле корреляции (рис. 4), из которого видно, что между показателями X и Y действительно наблюдается линейная связь.

Рис. 4. Поле корреляции

Составим расчетную табл. 7 и найдем суммы по всем столбцам.

Используя полученные суммы по столбцам, вычислим средние значения, средние квадратические отклонения и коэффициент корреляции:

.

.

Определим — параметры уравнения линейной регрессии:

Таблица 7. Расчетная таблица.

Проведем анализ полученных результатов. Расчеты подтвердили, что между прибылью Y и среднегодовой численностью промышленно-производственного персонала наблюдается положительная линейная корреляционная связь (r=0,84). Ожидаемое среднее значение прибыли при заданной численности производственного персонала можно оценить с помощью выборочного уравнения линейной регрессии:

Подставив значения X в уравнения регрессии, рассчитаем прогнозные значения (Yпр) прибыли от реализации для каждого наблюдения (см. табл. 7).

Коэффициент регрессии b1=0,025 показывает, что при изменении среднегодовой численности персонала на 1% прибыль от реализации увеличивается на 0,025 млн руб. Коэффициент детерминации, что означает, что 70,56% вариации признака Y объясняется вариацией независимой переменной X, а 29,44% вариации вызвано воздействием неучтенных в модели случайных факторов.