Парна регресія. 
Множинна лінійна регресія з урахуванням мультиколінеарності

1. За кореляційним полем вибираємо вигляди залежності.

За виглядом кореляційного поля (тому що з ростом x y, в основному, збільшується) припускаємо наявність залежності двох типів:

Прямолінійна.

; (5.1).

Експоненціальна.

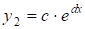
. (5.2).

2. Використовуючи метод найменших квадратів (МНК), знайдемо оцінки параметрів моделей, , і .

Відомо, що для лінійної моделі оцінки параметрів рівняння визначаються за формулами 5.3 і 5.4:

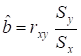
(5.3).

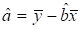
(5.4).

де rxy — вибірковий парний коефіцієнт кореляції поміж x і y;

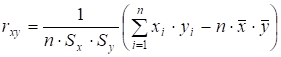
(5.5).

Sy, Sx — вибіркові середні квадратичні відхилення; визначаються як корінь квадратний із вибіркових дисперсій і :

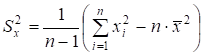
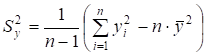
; (5.6).

 — вибіркові середні.

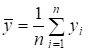
;.(5.7).

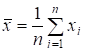
Таблиця з розрахованими значеннями наведена нижче:

Тоді отримана лінійна модель набуває вигляду:

y = + Ч X.

Для визначення оцінок і приведемо рівняння експоненціальної залежності до лінійного вигляду, прологарифмувавши його. Одержуємо. Здійснивши відповідні заміни й, одержимо лінійну залежність вигляду .

Розрахунки оцінок параметрів і проміжних величин зробимо за формулами (5. 3−5. 7) для лінійної моделі.

Тоді оцінка параметра і отримана експоненціальна модель приймає вигляд:

y = Ч e Чx.

3. Виберемо з двох отриманих залежностей найкращу. Критерієм оптимальності можна прийняти величину дисперсії залишків:

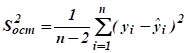
(5.8).

де — розрахункове значення, отримане для по моделі з визначеними оцінками параметрів.

Тоді дисперсія залишків складе:

для лінійної моделі ;

для експоненціальної моделі .

Тому що значення дисперсії залишків для лінійної моделі більше, ніж значення дисперсії залишків експоненціальної моделі, то перша модель гірше ніж друга наближає істинне значення y. Тому модель, що найбільше відбиває добре дану залежність, приймається отримана експоненціальна модель.

y = Ч e Чx .

4. У даному випадку оцінки параметрів моделі можна перевірити на значущість відмінності від нуля за значущістю коефіцієнта кореляції r із використанням критерію Стьюдента.

Розрахункове значення критерію.

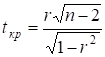
(5.9).

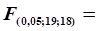
2,2. tроз= .

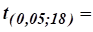
Табличне значення знаходимо за таблицею t-розподілу для імовірності a= 0,05 і числа ступенів свободи k = n-2 = 20−2 = 18, 2,1.

Отже, коефіцієнт кореляції r, а значить і d, суттево відрізняється від нуля з надійністю Р = 1-a = 1−0,05 = 0,95.

Тому що розрахункове значення критерію Стьюдента більше за табличний, то параметр d суттєво відрізняється від нуля.

5. Адекватність отриманої моделі експериментальним даним перевіримо за критерієм Фішера. Розрахункове значення критерію визначається як відношення дисперсій:

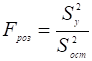
(5.10).

Fроз = .

Табличне значення знаходимо за таблицею F-розподілу для імовірності a = 0,05 і числа ступенів свободи k1 = m = 19 і k2 = n-m-1 = 20−2 = 18.

Тому що розрахункове значення критерію Фішера більше табличного, обрану модель можна вважати адекватною.

6. Проведемо аналіз отриманої експоненціальної залежності.

Коефіцієнт еластичності для отриманої моделі буде дорівнювати:

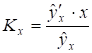
.(5.11).

Підставивши рівняння залежності в [5.11] одержимо:

.

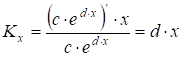
Тоді при зміні x для вихідних даних в інтервалі Ј х Ј коефіцієнт еластичності буде змінюватися в межах Ј Kx Ј. Таким чином, збільшення значення фактора на 1% викликає ріст значення показника в середньому на %.

Значення коефіцієнта кореляції, наближене до 1, а також мале значення величини дисперсії залишків означають тісний взаємозв'язок між фактором і показником. Оцінка значущості відмінності від нуля параметра рівняння й адекватності моделі дозволяють зробити висновок, що модель можна використовувати з метою прогнозування величини показника.

Лабораторна робота № 2.

Множинна лінійна регресія з урахуванням мультиколінеарності.

Регресійне рівняння (модель залежності) задовільно описує зміни залежної перемінної тоді, коли коефіцієнт множинної кореляції досить великий, а кореляція між факторами незначна. Мультиколінеарність факторів веде до обмеженості оцінок параметрів, тобто неможливості коректної інтерпретації результатів. Тому перед пошуком оцінок параметрів варто перевірити систему факторів на мультиколінеарність.

Один із методів перевірки факторів на мультиколінеарність — алгоритм Фарара-Глобера. Спочатку за допомогою c2 — статистики робиться перевірка всієї системи факторів на мультиколінеарність (із використанням кореляційної матриці). Якщо система факторів мультиколінеарна, то з використанням F-статистики перевіряється кожний фактор на мультиколінеарність. Далі за допомогою t-статистики перевіряються всі пари факторів на колінеарність. Серед мультиколінеарних пар виявляють мультиколінеарні фактори, що приводять до мультиколінеарності всю систему. Їх виключають із системи, якщо це не суперечить економічному змісту досліджуваної залежності. У іншому випадку переходять до іншої кількісної характеристики даного фактора.

Спочатку визначимо:

середні арифметичні значенняфакторів X, Y, Z і показника y;

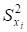
вибіркові дисперсії факторів і показника (формула 1.6 із завдання 1);

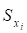
вибіркові середні квадратичні відхилення показника і факторів .

парні коефіцієнти кореляції відповідно до формули 1.5 у завданні 1.

Проведемо розрахунки відповідно до алгоритму Фаррара-Глобера для даної системи факторів (X, Y, Z).

1. Запишемо кореляційну матрицю системи факторів:

• 2. Знайдемо визначник матриці |R| = 0,0096 .
• 3. Визначимо розрахункове значення критерію c2 за формулою

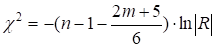
(5.12).

де n — об'єм вибірки;

m — число факторів у моделі.

Табличне значення c2 визначаємо, використовуючи таблицю критичних точок розподілу c2 у будь-якому підручнику (довіднику) з економетрії та математичної статистики.

У даному випадку:

розрахункове значення c2роз= ;

табличне (критичне) значення c2кр = c2(0,05; mЧ (m-1)/2) = 7,8.

Тому що c2расч і c2кр, то система факторів мультиколінеарна.

Далі визначаємо мультиколінеарні фактори.

2. Знаходимо матрицю С, зворотну кореляційній матриці R:

3. Розраховуємо F-статистики для факторів X, Y, Z за формулою:

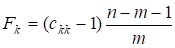
(5,13).

де сkk — елементи головної діагоналі матриці С.

Знаходимо табличне значення Fкр, використовуючи таблицю F-розподілу в будь-якому підручнику (довіднику) з економетрії та математичної статистики.

Якщо розрахункова F-статистика фактора більше критичного значення Fкр або дорівнює йому, то даний фактор мультиколінеарний.

У даному випадку:

фактор X — мультиколінеарний;

фактор Y — немультиколінеарний;

фактор Z — мультиколінеарний.

5. Визначимо мультиколінеарні пари факторів із використанням t-статистики (критерію Стьюдента).

Розрахункові значення t-статистик визначаються за формулою:

регресія мультиколінеарність парний.

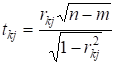
(5.14).

де rkj — приватні коефіцієнти кореляції між парами факторів:

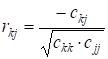
(5.15).

де сkj — елемент матриці С, що лежить у k-й рядку j-ом стовпці;

сkk і сjj — діагональні елементи матриці С.

У даному випадку:

Табличне значення tкр визначається за таблицею t-розподілу в будь-якому підручнику (довіднику) з економетрії і математичній статистиці.

У даному випадку:

Якщо розрахункове значення t-статистики пари факторів більше або дорівнює критичному, то дана пара факторів — мультиколінеарна.

У даному випадку:

пари факторів XY — немультиколінеарна;

пари факторів XZ — мультиколінеарна;

пари факторів YZ — немультиколінеарна.

З проведених розрахунків перевірки системи і факторів на мультиколінеарність очевидно, що фактор Z необхідно виключити з моделі для видалення властивості мультиколінеарності.

6. Визначимо оцінки параметрів моделі, використовуючи алгоритм стандартизованої моделі з b-коефіцієнтами.

Перепишемо кореляційну матрицю без коефіцієнта кореляції віддаленого фактора:

7. Знайдемо матрицю С, обернену кореляційної:

8. Обчислимо b-коефіцієнти:

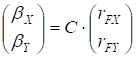
• (5.16)
• bX = ;
• bY =. .
• 9. Знайдемо коефіцієнт детермінації і множинної кореляції за формулою:

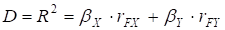
(5.17).

.

10. Для перевірки значущості відмінності від нуля b-коефіцієнтів за критерієм Стьюдента обчислимо розрахункові значення t-критерію за формулою.

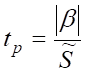
(5.18).

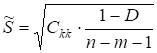
де .(5.19).

Табличне значення tкр знаходимо, використовуючи таблицю t-розподілу в будь-якому підручнику (довіднику) з економетрії та математичної статистики.

У даному випадку:

Якщо розрахункове значення більше або дорівнює табличному, то b-коефіцієнт значущий, тобто вплив фактора на показник істотний.

У даному випадку:

• bX — значущий;
• bY — значущий.

Отже, стандартизована модель набуде вигляду:

tF = Ч tx + Ч ty.

11. Переходимо від стандартизованої моделі до нормалізованого вигляду:

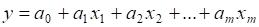
• (5.20)
• а) визначимо оцінки параметрів a1, a2, …, am при xi за формулою:

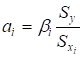
(5.21).

У даному випадку: a1 =; a2 = ;

б) визначимо оцінку вільного члена а0 за формулою:

а0 = Fсеред — а1Xсереда2Yсеред а0 =. .

Таким чином, рівняння залежності набуде вигляду:

F = + Ч X + Ч Y ;

в) перевірка адекватності отриманої моделі (значущості відмінності від нуля D) здійснюється з використанням розрахункового значення критерію Фішера, за формулою:

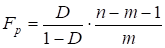
Fp =; Fкр = F (0.05; m; n-m-1) = 3,59.

Якщо розрахункове значення критерію Фішера більше або дорівнює табличному, то D — значуще, і отримана залежність адекватна експериментальним даним, її можна використовувати для прогнозування економічних показників.

Таким чином, одержали рівняння лінійної залежності показника F від факторів X і Y:

F = + Ч X + Ч Y.