Метод Гаусса-Зейделя.
Характеристика алгоритмів для вирішення поставленої задачі

Алгоритм послідовна програма паралельний Задамо деякі початкові (нульові) наближення невідомих, ,. Підставляючи ці значення в праву частину виразу (1.7), отримуємо нове (перше) наближення для: Припустимо, що діагональні елементи,, відмінні від нуля (в іншому випадку можна переставляти рівняння). Виразимо невідомі,, відповідного з першого, другого і третього рівнянь системи (1.6): Ітераційний… Читати ще >
Метод Гаусса-Зейделя. Характеристика алгоритмів для вирішення поставленої задачі (реферат, курсова, диплом, контрольна)
Одним з найпоширеніших ітераційних методів, який відрізняється простотою та легкістю програмування, є метод Гаусса-Зейделя. Проілюструємо спочатку цей метод на прикладі розв’язання системи.
(1.6).
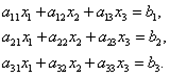
Припустимо, що діагональні елементи, , відмінні від нуля (в іншому випадку можна переставляти рівняння). Виразимо невідомі, , відповідного з першого, другого і третього рівнянь системи (1.6):
(1.7), (1.8).
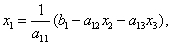
(1.9).
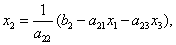
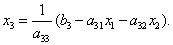
алгоритм послідовна програма паралельний Задамо деякі початкові (нульові) наближення невідомих:, ,. Підставляючи ці значення в праву частину виразу (1.7), отримуємо нове (перше) наближення для :
(1.10).
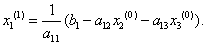
Використовуючи це значення для і наближення для, знаходимо з (1.8) перше наближення для :
(1.11).
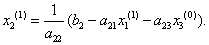
І нарешті, використовуючи обчислені значення, знаходимо за допомогою виразу (1.11) перше наближення для :
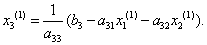
(1.12).
На цьому закінчується перша ітерація розв’язання системи (1.7) — (1.9). Використовуючи тепер значення, ,, можна таким же чином провети другу ітерацію, в результаті якої будуть знайдені другі наближення до розв’язку:, , і т.д. Наближення з номером можна представити у вигляді.
(1.13).
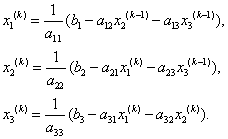
Ітераційний процес продовжується до тих пір, поки значення, , не стануть близькими з заданою похибкою до значень, , .