Уточнення наближеного розв'язку рівняння методом Ньютона

Рисунок 1.5 — Геометрична інтерпретація пошуку розв’язку рівняння методом Ньютона: а — для увігнутої функції; б — для опуклої функції. Для обчисленняx 2 у співвідношенні (1.6) слід замінити x0 на x1, аx1 — на x2, що утворить формулу для другого наближеного значення: Границя послідовності x0, x1, …, xn, …, через її монотонність та обмеженість, існує й дорівнює розв’язкові рівнянняf (x) =0… Читати ще >
Уточнення наближеного розв'язку рівняння методом Ньютона (реферат, курсова, диплом, контрольна)
Нехай функція f (x) задовольняє на відрізку [а,b] таким умовам:
- 1) рівняння f (x) =0 має єдиний розв’язок x;
- 2) функції f' (x) та f'' (x) є неперервні і зберігають знаки.
З першої умови випливає, що f (a) та f (b) мають протилежні знаки, а друга умова означає, що функція f (x) на відрізку [а,b] чи то лише зростає (f' (x) >0), чи лише спадає (f' (x) <0) і при цьому її графік є чи то увігнутим (f'' (x) >0), чи опуклим (f'' (x) <0). Тут можливі лише два випадки:
1) f (b) Чf'' (b) >0,f (a) Чf'' (a) >0.
У першому випадку графік функції y = f (x) має вигляд такий, як на рис. 1.5, а, а у другому — як на рис. 1.5, б. У першому випадку за початкове (нульове) наближення візьмемо точку х0=b і віднайдемо точку В= f (b). Далі проведемо з точки В дотичну до графіка f (x), точку перетинання якої з віссю абсцис позначимо x1. Це буде перше наближення. Відновлюючи з точки х1 перпендикуляр до перетинання з функцією f (x), віднайдемо точку В1. З цієї точки знов проведемо дотичну до функції f (x), віднайдемо точку її перетинання з віссю абсцис — x2, яка стане другим наближенням до розв’язку рівняння. Продовжуючи цей процес, обчислимо послідовність точок х3, х4,…, хn, яка наближається до розв’язку x рівняння (1.1).
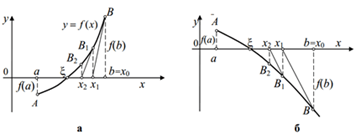
Рисунок 1.5 — Геометрична інтерпретація пошуку розв’язку рівняння методом Ньютона: а — для увігнутої функції; б — для опуклої функції.
Для віднаходження значення x1 складемо рівняння дотичної до графіка f (x) в точці B:
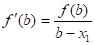
.
Враховуючи, що b= x0, обчислимо:
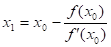
(1.6).
Для обчисленняx 2 у співвідношенні (1.6) слід замінити x0 на x1, аx1 — на x2, що утворить формулу для другого наближеного значення:
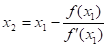
Продовжуючи цей процес для xn, обчислимо.
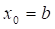
n= (1,2,3,…) (1.7).
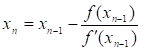
Границя послідовності x0, x1, …,xn, …, через її монотонність та обмеженість, існує й дорівнює розв’язкові рівнянняf (x) =0.
- 1) Вочевидь, що, якщо f (a) ?f" (a) >0, то слід покласти x0=a, і тоді формула (1.7) для обчислення xn залишається чинною.
- 2) Якщо застосувати метод Ньютона для кінця відрізка [a,b], на якому функція та її друга похідна мають протилежні знаки, то, замість наближення до розв’язку x, станеться віддалення від нього.