Застосування диференціального числення для дослідження функції

«Застосування диференціального числення для дослідження функції»

Монотонність функції.

Теорема 1. (Достатні умови строгої монотонності). Якщо функція.

f (x) диференційована на інтервалі (а; в); f (x) > 0 (f1 (x) < 0) всюди, крім, можливо, скінченого числа точок, в яких f1 = 0 на (а; в), то функція f (x) зростає (спадає) на (а; в) Доведення.

Нехай для визначеності f1 (x) > 0 і х1 та х2 дві довільні точки з (а; в), причому х 1 < х 2. Тоді на відрізку виконуються усі умови теореми Лагранжа, тому f (x2) — f (x1) = f 1 © (x2 — x1), с є (х1; х2).

За умовою f 1 © > 0, x2 — x1 > 0, тому f (x2) — f (x1) > 0 або.

f (x2) > f (x1), тобто функція f (x) на інтервалі (а; в) зростає.

Аналогічно доводиться теорема, якщо f 1 (х) < 0.

Теорема 2. (необхідна умова зростання).

Якщо диференційована на інтервалі (а; в) функція зростає, то f 1 (х)? 0.

на (а; в) Доведення.

Дійсно, нерівність f (x) < 0 неможлива — це суперечило б теоремі 1, отже, х є (а; в): f 1 (x)? 0.

З цього видно, що інтервали монотонності можуть відділитися один від одного або точками, де похідна дорівнює нулю (їх називають стаціонарними точками), або точками, де похідна не існує. Точки, в яких похідна дорівнює нулю або не існує, називають критичними точками першого ряду.

Не кожна критична точка відділяє інтервали монотонності.

Теорема 2 має такий геометричний зміст. Якщо на інтервалі (а; в) функція f (х) зростає, то дотична до кривої у = f (х) у кожній точці х є (а; в) утворює з додатним напрямом осі Ох гострий кут ц або (в окремих точках) горизонтальна; тангенс цього кута невід'ємний:

f 1 (x) = tg ц? 0. (Рис. 1).

Якщо на інтервалі (а; в) функція f (х) спадає, то кут нахилу дотичної тупий, або (в окремих точках) дотична горизонтальна; тангенс цього кута tg ц = f 1 (x)? 0 (Рис. 2).

у у х.

о, а в о, а в х Рис. 1. Рис.2

Інтервали монотонності можуть відділятися один від одного точками, де дотична або паралельна осі ОХ, або паралельна осі ОУ, або її не існує.

Отже, щоб знайти інтервали монотонності функції f (х), треба:

знайти область визначення функції;

знайти похідну даної функції;

знайти критичні точки з рівняння f 1 (x) = 0 та з умови, що f 1 (x) не існує;

розділити критичними точками область визначення на інтервалі і у кожному з них визначити знак похідної. На інтервалах, де похідна додатна, функція зростає, а де від'ємна — спадає.

Локальний екстремум функції.

функція перегин монотонність екстремум.

Точка х0 називається точкою локального максимуму (або мінімуму) функції f (x), якщо існує такий окіл 0 < < б Точки х0, який належить області визначення функції, і для х цього околу виконується нерівність f (x) f (x0)). Геометричний зміст означення показано на рисунку 3.

у Рис. 3 у.

F (x) F (x).

m.

i.

xoxo xo+ x о xoxo xo+ х Точки локального максимуму і локального мінімуму називають точками локального екстремуму, а значення функції в цих точках відповідно локальним максимумом і локальним мінімумом.

Теорема 1. (Необхідна умова локального екстремуму). Якщо функція f (x) має в точці х0 локальний екстремум і диференційована в цій точці, то f 1 (x0) = 0 .

Теорема 1має такий геометричний зміст. Якщо точки х1, х2, х3, х4- точки локального екстремуму і у відповідних точках графіка (Рис. 4) існують невертикальні дотичні, то ці дотичні паралельні осі ОХ.

у.

M.

m.

m a m.

max min x i.

n.

А х1×2×3×4 в х Рис. 4.

Умова f 1 (x0) = 0 є необхідною але в точці х0 функція мала локальний екстремум.

Це означає, що не всяка точка х0, в якій f 1 (x0) = 0, є екстремальною точкою.

Отже, повну необхідну умову локального екстремуму можна сформулювати так: якщо функція має в точці локальний екстремум, то ця точка є критичною.

Теорема 2. (Теорема достатня умова локального екстремуму). Нехай х0 — критична точка функції f (x), яка в цій точці неперервна, і нехай існує окіл (х0 — б; х0 + б) точки х0, в якому функція має похідну f 1(x) крім, можливо, точки х0, тоді:

якщо в інтервалі (х0 — б; х0) похідна f 1 (x) > 0, а в інтервалі (х0; х0 + б) похідна f 1(x) < 0, то х0 є точкою локального максимуму функція f (x);

якщо в інтервалі (х0 — б; х0) похідна f 1 (x) > 0, то х0 є точкою локального мінімуму функції f (x) ;

якщо в обох інтервалах (х0 — б; х0) і (х0; х0 + б) похідна f 1(x) має той самий знак, то х0 не є екстремальною точкою функції f (x).

Можна сказати так: якщо при переході зліва направо через критичну точку х0 знак похідної f 1(x) змінює з плюса на мінус, то х0 — точка локального максимуму; якщо знак похідної f 1(x) змінюється з мінуса на плюс, то х0 — точка локального мінімуму; якщо похідна не змінює знак, то в точці х0 екстремум відсутній.

З теорем 1 і 2 випливає правило дослідження функції на екстремум:

Щоб знайти локальний екстремум функції f (x), треба:

знайти критичні точки функції f (x).

Для цього слід розв’язати рівняння f 1(x) = 0; серед його розв’язків вибрати тільки ті дійсні корені, які є внутрішніми точками області існування функції; знайти точки, в яких похідна f 1(x) не існує;

якщо критичних точок функції не має, то вона не має і екстремумів.

Якщо критичні точки є, то треба дослідити знак похідної в кожному з інтервалів, на які розбивається область існування цими критичними точками. Для цього достатньо визначити знак похідної в якій — небудь одній точці інтервалу, оскільки похідна може змінити знак при переході через критичну точку;

за зміною знака f 1(x) при переході через критичні точки зліва направо визначити точки максимумів і мінімумів і обчислити значення функції f (x) в цих точках. Результати дослідження доцільно звести в таблицю.

Теорема 3. (Друга достатня умова локального екстремуму) Нехай х0 — стаціонарна точка функції f (x), тобто f 1(x0) = 0, і в околі точки х0 існує друга неперервна похідна, причому f 11(x0)? 0. Якщо f 11(x0) > 0, то х0 — точка локального мінімуму; якщо f 11(x0) < 0, то х0 — точка локального максимуму.

Як бачимо, дослідження функції на екстремум за другою умовою простіше, ніж за першою. Однак ця умова застосовується до вужчого класу функцій. Її не можна використовувати для дослідження тих критичних точок, в яких перша похідна не існує, а також до тих стаціонарних точок, в яких друга похідна дорівнює нулю.

Теорема 4. (Третя достатня умова локального екстремуму), Нехай в околі стаціонарної точки х0 існує інтервальна похідна f n (x), причому f n (x0)? 0,.

f 1(x0) = f 11(x0) =…= f (n-1)(x0) = 0. (1).

Тоді: 1) n — парне і f n < 0, то f (x) має в х0 локальний максимум;

• 2) якщо n — парне і f n > 0, то f (x) має в х0 локальний мінімум;
• 3)якщо n — непарне, то f (x) в х0 локального екстремуму не має.

Скориставшись відомою формулою Тейлора і взявши до уваги рівності (1) дістанемо:

f (x) — f (x0) = (х — х0) n (2).

де с лежить між х та х0.

Найбільше і найменше значення функції.

Розглянемо спочатку випадок, коли функція f (x) неперервна на відрізку .

Як відомо раніше, що така функція досягає своїх найбільшого і найменшого значень, які називають абсолютними екстремумами функції на цьому відрізку і позначають відповідно: М = max f (x), m = min f (x).

a<�х? в, а? х? в (3).

Щоб знайти найбільше (найменше) значення функції f (x), яка неперервна відрізку, треба:

знайти критичні точки функції f (x), які належать інтервалу (а; в);

обчислити значення функції f (x) у знайдених критичних точках і точках, а та в і серед цих значень вибрати найбільше (найменше).

Нехай функція f (x) неперервна на інтервалі (а; в), Така функція може й не мати абсолютних екстремумів. Про наявність їх судять з поводження даної функції на кінцях інтервалу (обчислюючи lim f (x), lim f (x)) та значення.

x > a + 0 x > в — 0.

f (x) в критичних точках, які належать інтервалу (а; в) Окупність і вгнутість кривих. Точки перегину Крива у = f (x) називається опуклою на інтервалі, якщо всі її точки, крім точки дотику, лежать нижче довільної її дотичної на цьому інтервалі.

Крива у = f (x) називається вгнутою на інтервалі, якщо всі точки, крім точки дотику, лежать вище довільної її дотичної на цьому інтервалі.

Точкою перегину називається така точка кривої, яка відділяє її опуклу частину від вгнутої.

Зрозуміло, що в точці перегину дотична перетинає криву, оскільки з одного боку околу цієї точки графік кривої знаходиться під дотичною, а другого — над дотичною.

Інтервали окупності і вгнутості знаходяться за допомогою такої теореми.

Теорема 1. Нехай функція у = f (x) є двічі диференційованою на (а; в), тоді:

якщо f 11(x) < 0; х є (а; в), то крива у = f (x) опукла на (а; в);

якщо f 11(x) > 0, х є (а; в), то крива у = f (x) вгнута на (а; в) З теореми 1. Випливає, що, а точці перетину друга похідна дорівнює нулю (якщо вона існує). Однак точками перегину кривої у = f (x) можуть бути також і точки, в яких друга похідна f 11(x) не існує.

Точки, в яких друга похідна f 11(x) дорівнює нулю або не існує, називається критичними точками другого ряду функції f (x). Отже, якщо х0 — абсциса точки перегину функції f (x), то х0 критичною точкою другого роду цієї функції.

Теорема 2. Нехай х0 — критична точка другого роду функції f (x).

Якщо при переході через точку х0 похідна f 11(x) змінює знак, то точка (х0; f (x0) є точкою перегину кривої f (x).

Щоб знайти точки перегину кривої, треба знайти критичні точки другого роду і дослідити зміну знака другої похідної при переході через ці точки.

Нехай існує б — окіл точки х0 такий, що х є (х0 — б; х0): f n (x) <0, то крива у = f (x) буде опукла на цьому інтервалі;

х є (х0; х0 + б): f 11(x) > 0, то крива у = f (x) буде вгнута на цьому інтервалі.

І точки (х0; f (х0)) будуть точками перегину.

Асимптоти кривої графіка функції.

Пряма е називається асимптотою кривої, якщо відстань б від змінної.

точки М кривої до цієї прямої прямує до нуля, коли точка М, рухаючись по кривій, віддаляється на нескінченність. Рис. 5.

l.

у у y.

l у=f (x).

м у=f (x) n p.

м.

o, а х о х o Q x.

y=f (x) a б в На рисунку 5 показано а) — вертикальну; б) — горизонтальну; в) — похилу асимптоти.

З означення асимптоти випливає, що для існування вертикальної асимптоти х = х0необхідно і достатньо, щоб lim f (x), =, або lim f (x) = ,.

x> x0 — 0 x> x0 + 0.

або lim f (x) =.

x> x0.

Дійсно в цьому випадку (Рис. 5 а).

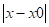
Б = = > 0 при х > х (4).

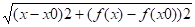
Рівняння похилої асимптоти буде шукатися у вигляді:

у = кх + в (5).

Знайдемо к та в. З рисунку 5 маємо б = МП, МN = =, тому, якщо б > 0 при х >, то МN > 0, і навпаки. Але МN = МQ — NQ = =f (x) — (кх + в), тому якщо при х > пряма у = кх + в є асимптотою, то lim (f (x) — кх — в) = 0 (5) або.

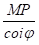
х >

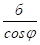
lim = 0 (7), тому х >

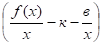
lim = 0, (8) звідки к = lim.

х > х >

Знайшовши к, з рівності (6) дістанемо в = lim (f (x) — кx) (9).

Отже, якщо існує похила асимптота (5), то к та в знаходяться за формулами (8) і (9) .

Навпаки, якщо існують скінченні границі (8) і (9), то виконуються рівність (6), тобто пряма (5) є похилою асимптотою.

Примітка 1. Якщо хоча б одна з границь (8) або (9) не існує, або дорівнює нескінченності, то крива похилої асимптота не має;

2. Якщо к = 0, то в = lim f (x), тому у = в — рівняння горизонтальної.

х >

асимптоти (Рис. 5 б). Оскільки це рівняння є окремим випадком рівняння (5), то розрізняють не три, а два види асимптот: вертикальні і не вертикальні.

Асимптоти кривої у = f (x) при х > + і х > - можуть бути різні. Тому при знаходженні асимптот границі (8) і (9) потрібно обчислювати при х > + і при х > - .

Загальна схема дослідження функції та побудова її графіка Щоб дослідити функцію та побудувати її графік, потрібно виконати слідуючі дії:

знайти область існування функції;

знайти (якщо це можливо) точки перетину графіка з координатними осями;

дослідити функцію на періодичність, парність і непарність;

знайти точки розриву та дослідити їх;

знайти інтервали монотонності, точки локальних екстремумів та значення функції в цих точках;

знайти інтервали окупності, вгнутості та точки перегину;

знайти асимптоти кривої;

побудувати графік функції, враховуючи дослідження, проведені в пунктах 1 — 7.

Якщо при побудові графіка виявиться, що він незрозумілий, то потрібно додатково знайти кілька точок графіка, обчислити значення функції при певних значеннях аргументу, бажано також в цих самих точках обчислити першу похідну, щоб визначити в них напрям дотичної.

Якщо дана функція періодична з періодом Т, то досить побудувати її графік на відрізку, після чого повторити цей графік на проміжку (n Т; (n + 1) Т),.

n = ± 1, ± 2, …

Якщо функція парна (непарна), то достатньо побудувати її графік для х 0, а потім відобразити його симетрично відносно осі ЩУ (або відносно початку координат).