Розділ 2. Рівняння Шредінгера для кристала

Тверде тіло, як відомо, складається з атомів, тобто з ядер атомів і електронів. Ядра атомів утворюють кристалічну решітку, яка володіє властивістю просторової періодичності. При накладанні зовнішнього електричного поля решітка практично не деформуються, хоча ядра атомів і заряджені. Це відбувається тому, що сили, що утримують ядра атомів у вузлах кристалічної решітки, звичайні значно більше тих сил, які створюються зовнішніми електричними полями. Ті з електронів, які не знаходяться близько до ядра атома і тому до нього не дуже сильно притягуються, можуть пересуватися по твердому тілу, створюючи електричний струм. Проте при кількісному описі цього явища виникають серйозні труднощі. Вони пов’язані з тим, що електрони є зарядженими частинками і при своєму русі по твердому тілу зустрічаються з іншими електронами. Але оскільки між електронами діють електричні сили відштовхування, той рух електрона виявляється залежним від руху електронів, що оточують його. Іншими словами, в даному випадку треба вирішувати не одноелектронну, а багатоелектронну задачу. Тому для визначення стаціонарних станів і енергетичного спектру сукупності більшого числа атомних ядер і електронів в кристалі потрібно розвязати рівняння Шредінгера:

HШ=- ЕШ (2.1),.

де H — гамільтоніан кристала; Ш — власна хвилева функція гамільтоніана; Е — енергія кристала.

Значення хвилевої функції кристала залежать від координат всіх електронів г_i і всіх атомних ядер Rб:

Ш = Ш (г₁, г₂.. ., г_n, R₁, R₂.. ., R_N). (2.2).

З урахуванням цих складових гамільтоніана рівняння Шредінгера прийме вигляд:

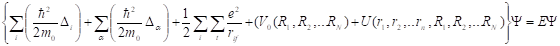
Число незалежних змінних в рівнянні визначається повним числом частинок в кристалі, які в 1 см³ речовини складають величину порядка 10²³. Таке завдання в даний час не може бути вирішена в загальному вигляді. Можливе лише наближене рішення задачі, яке досягається за допомогою ряду послідовних наближень.