Визначити кількість інформації у кожному із символів, знайти ентропію та надмірність джерела

Визначимо ентропію джерела та максимальну ентропію (формула 1.2): Де Hmax=log m — максимальна ентропія за розміру алфавіту m. Тоді надмірності визначимо за формулами 1.3−1.4: Таблиця 1.1 — Статистична схема джерела. Абсолютна надмірність: (1.3). Відносна надмірність: (1.4). Висновок. І5 == 4,322. І4 == 1,515. І3 == 2,322. І2 == 1,737. І1 == 3,322. Іі =(1.1). H (1.2). 11,11%. Hmax=. A5. A4. A3… Читати ще >
Визначити кількість інформації у кожному із символів, знайти ентропію та надмірність джерела (реферат, курсова, диплом, контрольна)
Джерела повідомлень характеризуються статистичною схемою (таблиця 1.1). Визначити кількість інформації у кожному із символів, знайти ентропію та надмірність джерела.
Таблиця 1.1 — Статистична схема джерела
a1 | a2 | a3 | a4 | a5 |
0,1. | 0,3. | 0,2. | 0,35. | 0,05. |
Кількість інформації в кожному з символів можна обчислити за формулою[2]:
Іі =(1.1).
Ентропія — це середня кількість інформації, яка припадає на один символ повідомлення. Ентропія визначається за формулою[1]:
H (1.2).
Надмірність коду повідомлення визначається за такими формулами[1]:
Абсолютна надмірність: (1.3).
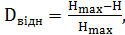
Відносна надмірність: (1.4).
де Hmax=log m — максимальна ентропія за розміру алфавіту m.
Знайдемо кількість інформації у кожному із символів (формула 1.1) :
І1 == 3,322.
І2 == 1,737.
І3 == 2,322.
І4 == 1,515.
І5 == 4,322.
Визначимо ентропію джерела та максимальну ентропію (формула 1.2) :
H.
Hmax=.
Тоді надмірності визначимо за формулами 1.3−1.4 :
=11,11%.
Висновок
Ентропія — це середня кількість інформації, яка припадає на один символ повідомлення вона завжди на перевищує log m. Ентропія починає зменшуватися якщо символи стають не рівноімовірними аж до нуля якщо імовірність появи одного з символів наближається до одиниці.
Надмірність показує відхилення справжньої ентропії від максимальної і може бути як абсолютна так і відносна.