Розділ 4. Неперервні відображення

Поняття функції

Означення 1.1. Нехай маємо дві множини Х і У. Якщо кожному елементу за певним законом ставиться у відповідність один і тільки один елемент у із множини У, то говорять, що на множині Х задана функція f (або відображення множини Х в множину У).

Записують так:. Якщо у відповідає х, то записують так:. Множина Х називається областю визначення функції f. Множина тих, які приймає функція, називається областю значень функції , — область значень, (не обов’язково). Якщо, говорять, що функція відображає множину Х на множину У.

Через будемо позначати прообраз множини (це множина А всіх тих х-ів з Х, що).

Границя і неперервність функції

Нехай маємо два метричні простори Х і У. Відстань в просторі Х будемо позначати, в просторі У — ₁.

Нехай множина М міститься в Х,, на множині М задана функція, яка відображає множину М в У, гранична точка множини М.

Означення 2.1. Елемент b простору У, називається границею функції f, коли х прямує до, якщо для довільного існує таке, що для будь-якого х із множини М, яке задовольняє умові, виконується нерівність: .

Дане означення евівалентне наступному.

Означення 2.2. Елемент b простору У, називається границею функції f, коли х прямує до, якщо для довільної послідовності вилученої з М, причому, яка збігається до, відповідна послідовність значень функції збігається до b.

Еквівалентність обох означень доводиться як і для дійсних функцій.

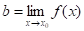
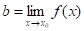
Якщо b — границя функції f при х, прямуючому до, то записують так:, іноді пишуть, коли. Якщо, то це геометрично означає, що який би ми окіл точки b не взяли, то знайдеться проколотий окіл точки х₀ такий, що якщо х попаде в цей проколотий окіл, то f (x) попадає у вибраний окіл точки b (проколотий окіл точки х₀ — це окіл точки х₀ з якого вилучено точку х₀).

Означення 2.3. Функція f,, називається неперервною в точці, якщо для довільного, існує, таке, що для всіх х з множини М, які задовільняють умові, визначається нерівність .

Якщо є граничною точкою множини М, то це означення еквівалентне наступному.

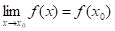
Означення 2.4. Функція f називається неперервною в точці, якщо .

Еквівалентність обох означень для цього випадку очевидна.

Означення 2.5. Функція f, яка відображає множину М метричного простору Х в метричний простір У, називається неперервною на множині М, якщо вона неперервна в кожній точці цієї множини.

Означення 2.6. Функція f, , називається рівномірно неперервною на множині М, якщо для довільного, існує таке, що для будь-яких х₁ і х₂ із множини М, які задовольняють умові, виконується рівність .

Якщо f рівномірно неперервна на М, то вона і неперервна на цій множині. Обернене твердження взагалі невірне.

Теорема 2.1. (Критерій неперервності). Для того, щоб відображення f:XY було неперервним в Х, необхідно і достатньо, щоб прообразом будь-якої відкритої множини простору У була відкрита множина простору Х.

Доведення. Необхідність. Нехай f неперервне відображення і G відкрита множина простору У, f ^-1(G) прообраз G. Якщо f ^-1(G) є порожньою множиною, то все зрозуміло, бо порожня множина є відкритою множиною. Нехай f ^-1(G) і х₀ f ^-1(G). Тоді у₀=f (x₀) G. Оскільки G відкрита множина, то існуєокіл S (y₀;) точки у₀, який повністю лежить в G. Так, як відображення f неперервне в точці х₀, то існуєокіл цієї точки такий, що для всякого х з цього околу, f (x) належить S (y₀,). Отже всі точкиоколу точки х₀ належать f —¹(G), а це означає, що х₀ внутрішня точка f —¹(G), а f —¹(G) є відкритою множиною.

Достатність. Нехай прообразом будь-якої відкритої множини є відкрита множина. Покажемо, що f неперервна функція в G. Нехай х₀Х, у₀=f(x₀)Y. Візьмемо довільнийокіл S (f (x₀),) точок f (x₀). Оскільки він є відкритою множиною, то його прообразом є відкрита множина, яка містить точку х₀. Тому існуєокіл S (x₀,) точки х₀, який повністю міститься в f —¹(G). А це означає, що f є неперервною функцією в точці х₀, а отже і в просторі Х. Теорему доведено.