Виключення спільного виразу

Якщо в обох рівнянь системи входить одне і теж вираження, то можна виключити це вираження, тобто з одного рівняння знайти це вираження і підставити в інше рівняння. При цьому може знайтися більш просте рівняння.

Приклад. Розв’яжемо систему рівнянь.

Запишемо цю систему рівнянь у вигляді.

В обидва рівняння входить вираз. Крім цього виразу отримаємо вираз.

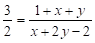
або.

Підставивши у друге рівняння вираз вихідної системи і отримаємо.

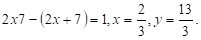
Приклад. Розв’яжемо систему рівнянь.

Запишемо систему рівнянь у вигляді.

Крім спільного виразу, отримаємо, .

Розв’язуючи останню систему, знаходимо рішення .

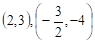
Приклад. Розв’яжемо систему рівнянь.

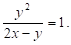
Друге рівняння можна записати у вигляді.

В обидва рівняння ходить вираз. Перемножуючи рівняння, виключаємо вираз і приходимо до рівняння.

яке має рішення:

Система рівнянь з модулями

При розв’язанні рівнянь з модулями не використовувати визначення модуля числа.

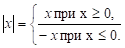
Приклад. Знайти рішення системи рівнянь.

Робимо все можливі припущення про значення чисел.

1. Нехай Система рівнянь має вид.

і має рішення:

2. Нехай Отримаємо систему рівнянь.

.

яка має рішення:

3. Нехай. Отримаємо систему рівнянь яка має розв’язок:

4. Нехай. Отримаємо систему рівнянь яка має рішення: