Згладжування часових рядів зваженим ковзким середнім. 
Критерій Аббе

Мета згладжування часового ряду — виділення його детермінованої складової,. Одним з найбільш поширених способів згладжування часового ряду є його обробка із застосуванням процедури зваженого ковзкого середнього. В загальному вигляді процедуру обчислення згладженої оцінки для t-ого рівня ряду описує вираз:

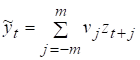
(48).

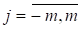
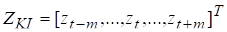
де , — вагові коефіцієнти згладжуючого фільтру — рівні ряду, що утворюють так званий ковзкий інтервал (КІ) довжиною 2m+1, який отримав назву завдяки своєму покроковому переміщенню вздовж часового ряду у ході виконання згладжування останнього. Покрокове переміщення КІ здійснюється шляхом відкидання його крайнього лівого елементу та приписування до КІ справа найближчого сусіднього рівня часового ряду. При такому зміщенні КІ черговий згладжуваний рівень ряду опиняється у середині КІ, тобто оцінка завжди обчислюється для середини КІ. Через це m перших та m останніх рівнів часового ряду залишається незгладженими. Це явище отримала назву крайового ефекту.

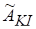
Для отримання згладженої оцінки за даними КІ будується поліноміальна модель виду (41), яка має апроксимувати фрагмент часового ряду в межах ковзкого інтервалу. Для цієї моделі розраховується вектор МНК-оцінок параметрів, який далі використовується для обрахування згладженої оцінки в середній точці КІ. Отримана оцінка є шуканою згладженою оцінкою t-ого рівня часового ряду. За аналогією з (46) маємо:

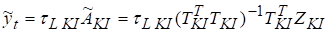
(49).

де — середній рядок матриці плану .

Зважаючи, що довжина 2m+1 ковзкого інтервалу та порядок р поліному (41) залишаються незмінними впродовж всієї обробки часового ряду, незмінною буде і матриця плану, тому матричний добуток у правій частині виразу (49), пов’язаний лише з параметрами m та р, можна обрахувати заздалегідь:

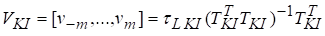
. (50).

Зробивши відповідну заміну у співвідношенні (49):

.

отримуємо матричну форму запису виразу (48), тобто — вектор вагових коефіцієнтів згладжуючого фільтру. Властивість сталості значень вагових коефіцієнтів при заданих параметрах m та р фільтрів дозволяє виконати попереднє обрахування ваг для різних сполучень m та р та внести отримані значення векторів до довідкових розділів спеціалізованої літератури [4].

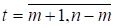
Для практичної реалізації процедури згладжування актуальне питання вибору параметрів m, р згладжуючого фільтру. Звичайно воно розв’язується шляхом підбору значень m, р за допомогою критерію якості згладжування. Методичною базою цього перебору може бути викладена у розділі 7.1 ідея перевірки автокорельованості нев’язок,. Саме ця ідея реалізована у критерії Аббе, який можна застосувати для вибору параметрів фільтру:

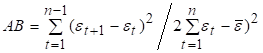
(51).

де — середнє арифметичне значення нев’язок.

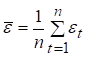
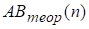
Якщо, то приймається гіпотеза некорельованості нев’язок, тобто якісного згладжування. Теоретичне значення для n>60 розраховується за формулою:

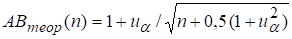
(52).

де — б-квантиль нормованого нормального розподілу. При значення для трьох найбільш застосовних рівнів значущості б наведено в [18].

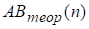
Зазначимо, що оцінку дисперсії нев’язки, отриману для найближчого до 1 значення статистики Аббе, можна вважати найбільш точною оцінкою дисперсії стохастичної складової еt часового ряду:

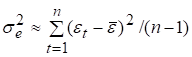
. (53).