Загальне (часове) рівняння Шредінгера

У класичній механіці рівняння одновимірного руху частинки дозволяє одержати її координату x (t) і імпульс p (t) за їх початковими значеннями x (0) і p (0). Таким рівнянням руху є другий закон Ньютона.

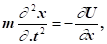
(1.2.11).

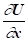
де m Ї маса частинки; Ї прискорення руху частинки; Ї градієнт потенціальної енергії, зміна якої визначається діючою силою.

З визначення квантового стану рівняння руху квантової частинки має задавати зміну в часі хвильової функції. Оскільки квантовий стан характеризує лише одна хвильова функція, то відповідне квантове рівняння руху повинно містити лише першу похідну за часом від хвильової функції. В інших випадках таке рівняння не буде погоджуватись з визначенням квантового стану .

Рівняння руху квантової нерелятивістської частинки в силовому полі називається рівнянням Шредінгера, тому що вперше в 1926 році воно було сформульовано німецьким фізиком Е. Шредінгером.

Справедливість цього рівняння обґрунтована тим, що всі висновки які випливають із нього, знайшли своє експериментальне підтвердження. Рівняння Шредінгера відіграє у квантовій механіці таку ж роль, як і рівняння Ньютона в класичній.

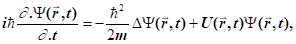
У загальному випадку часове рівняння Шредінгера має вигляд.

(1.2.12).

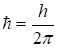
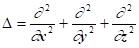
де m Ї маса частинки; Ї потенціальна енергія частинки в сило-вому полі; Ї уявна одиниця; Ї стала Дірака; Ї оператор Лапласа.

Через присутність в рівнянні Шредінгера (1.2.12) уявної одиниці хвильова функція, яка задовольняє це рівняння, завжди комплексна. Не кожна функція може бути розв’язком рівняння (1.2.12). Перш за все ця функція повинна бути скінченною, неперервною і мати неперервні перші похідні. Ці вимоги мають чисто математичний характер. Крім того — хвильова функція повинна бути однозначною, інакше буде порушений її статистичний зміст.

Рівняння Шредінгера за часом є лінійним диференціальним рівнянням 1-го порядку. З теорії диференціальних рівнянь відомо, що кожне лінійне рівняння в частинних похідних повинно мати безліч розв’язків, причому таких, що всяка лінійна комбінація будь-якої сукупності розв’язків теж буде його розв’язком.

Слід зауважити, що рівняння Шредінгера, подібно до законів Ньютона в класичній механіці, не є результатом якогось теоретичного доведення, а є узагальненням багатьох дослідних фактів, встановлених при вивченні мікросвіту. Відмітимо також, що рівняння Шредінгера описує рух частинок, швидкість яких значно менша швидкості світла, оскільки співвідношення між кінетичною енергією й імпульсом справедливе лише при цих умовах. У релятивістському випадку для описання хвильових властивостей мікрочастинок слід користуватись іншими рівняннями, наприклад рівняннями Дірака або Клейна Ї Гордона.