Види рівнянь прямої на площині

Пряма на площині геометрично може бути задана різними способами: точкою і вектором, паралельним даній прямій; двома точками; точкою і вектором, перпендикулярним до даної прямої, загальним рівнянням, тощо.

Нехай пряма проходить через задану точку Мо паралельно заданому ненульовому вектору S, який називається напрямним вектором прямої. Пряма має безліч напрямних векторів, їхні відповідні координати пропорційні. Точка Мо і її напрямний вектор цілком визначають пряму, тому що через точку Мо можна провести лише 1 пряму, паралельну вектору S.

Змінна t у формулі (2) може набувати довільних дійсних значень і називається параметром, а рівняння (2) називається векторним параметричним рівнянням прямої.

Векторне параметричне рівняння прямої має однаковий вигляд і на площині, і в просторі.

Якщо пряма L розглядається на площині і задається точкою Мо (х о, уо) та напрямний вектором S = (m, n), то порівнюючи відповідні координати векторів r та ro + st за формулою (2).

маємо: х= х_о+ mt; у= у_о+ nt (3) звідси.

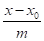
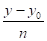
= (4).

Рівняння (3) називають параметричним рівнянням прямої, а рівняння (4) її канонічним рівнянням.

Якщо пряма проходить через точку Мо (хо, уо) паралельно осі Ох, то її напрямний вектор S = (m, o), тому рівняння (4) набуває вигляду.

=.

Розв’язавши його, ми одержимо (у-уо) m=(х-хо) 0; (у-уо) m=0 у=уо — це і є рівняння прямої, яка паралельна осі ОХ.

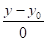
Аналогічно, якщо пряма проходить через точку Мо (х о, уо) паралельно осі ОУ, то її рівняння буде мати вигляд: х=хо.

Виведемо рівняння прямої з кутовим коефіцієнтом. Якщо пряма не перпендикулярна до осі ОХ, то рівняння (4) можна записати у вигляді.

у-у_о= (х-х_о) або у= х+(у_о х_о).

Позначимо к=; в= уо х, одержимо:

(5) у-у_о= к (х-х_о) або у= кх+в (6).

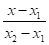
к = =tgб, де б — кут утворений прямою з додатним напрямком осі ОХ називається кутовим коефіцієнтом прямої, а величина в=уохо ордината точки перетину прямої з віссю ОУ. Якщо пряма проходить через початок координат, то в=0 і рівняння такої прямої має вигляд у=кх (7).

Рівняння (5) називається рівнянням прямої. Яка проходить через задану точку і має заданий кутовий коефіцієнт.

Рівняння (6) називається рівнянням прямої з кутовим коефіцієнтом. Якщо пряма проходить через 2 задані точки М1(х1, у1) та М2(х2, у2) дістанемо з рівняння прямої, що проходить через точку М1 і має напрямний вектор S = М1М2 = (х2-х1; у2-у1).

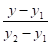
= (7) — це і є рівняння прямої, що проходить через 2.

Якщо пряма проходить через задану точку Мо (х о, уо) перпендикулярно заданому вектору S = (АВ), як показано на рис. 3.

На прямій L візьмемо точку М (х, у) і розглянемо вектор Мо М=(х-хо; у-уо). Вектори ММо та S перпендикулярні, тому їх скалярний добуток дорівнює 0, тобто:

А (х-хо) + В (у-уо) = 0 8.

Будь-яка точка прямої з відповідними координатами задовольняють рівняння 8, а координатами точки, що не лежать на цій прямій, не задовольняють рівняння 8. Тому, ц у це рівняння є рівнянням прямої, що проходить через точку Мо (х о, уо) перпендикулярно вектору S = (АВ).

Якщо пряма проходить через точки з координатами, А (а, 0) та В (о, в), тобто відтинає на осях відрізки, а і в, як показано на рис. 3, то з рівняння (7) маємо:

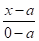
= або + = 1 (9).