Теорема М.Є.Жуковського.
Кінетостатичний аналіз механізмів

Якщо помножити всі складові цього рівняння на масштаб, маємо швидкості точок: Позначимо плечі сил, а також кути між векторами швидкостей та цими плечами. Із плану швидкостей бачимо, що плечі сил, можна виразити таким чином: Складаємо рівняння суми моментів усіх сил відносно полюса плану. Сума елементарних робіт на можливих переміщеннях дорівнює нулю. Запишемо остаточно рівняння у формі… Читати ще >
Теорема М.Є.Жуковського. Кінетостатичний аналіз механізмів (реферат, курсова, диплом, контрольна)
М.Є.Жуковський — видатний російський вчений в галузі механіки, аеродинаміки та гідродинаміки, теорії авіації. У курсі ТММ розглядаються дві його теореми. Розглянемо одну з них:
Якщо зрівноважену систему сил, що діють на ланки механізму, перенести в однойменні точки повернутого на 900 плану швидкостей механізму, то сума моментів цих сил відносно полюса плану дорівнює нулю.
Доведемо цю теорему (див. рис. 5.13):
- 1. Нехай маємо механізм, на ланки якого діють сили ., що є рівнодіючими всіх сил і прикладені відповідно в т. (рис. 5.13,а).
- 2. На повернутий на 900 план швидкостей у однойменні точки (знайдені за подібністю) переносимо сили (рис. 5.13,б).
- 3. Для доведення теореми скористаємося принципом можливих переміщень, відомий з курсу теоретичної механіки.
Сума елементарних робіт на можливих переміщеннях дорівнює нулю.
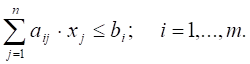
. (5.43).

Треба довести, що .
- 4. Позначимо плечі сил, а також кути між векторами швидкостей та цими плечами.
- 5. Складаємо рівняння суми моментів усіх сил відносно полюса плану .
Скористаємося поняттям доведення від зворотного, тобто прирівнюємо суму моментів сил не нулю, а деякій величині А, далі треба довести, що .

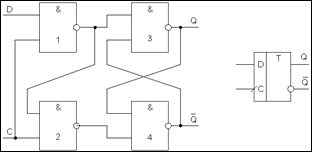
Рис. 5.13: До теореми Жуковського:
а. — план механізму; б. — план швидкостей, повернутий на 900
6. Із плану швидкостей бачимо, що плечі сил, можна виразити таким чином:
. (5.44).
7. Якщо помножити всі складові цього рівняння на масштаб, маємо швидкості точок :
.
або. (5.45).

8. Розглянемо, що це за кути. Для цього переносимо вектори швидкостей на план механізму в точки, повертаючи їх попередньо на кут 900 проти напряму повороту плану швидкостей (рис. 5.13,б). Як бачимо, це кути між векторами сил і векторами швидкостей (два останніх — між їх продовженнями).

9. Помножимо всі частини попереднього рівняння на (у лівій частині отримаємо елементарні переміщення точок), а також урахуємо знаки «cos»:

(5.46).
Примітка: знаки «+» з’явилися за рахунок напрямів швидкостей.
10. Запишемо остаточно рівняння у формі «елементарних переміщень»:
11. У реальному механізмі всі елементарні переміщення є й можливими, отже:, але, отже,, що й треба було довести.