Вправи. 
Функції і їх графіки

Для функцій, графіки яких зображені на рисунку 14.26, а-г, знайдіть:

• а) проміжки зростання й спадання функції;
• б) точки максимуму і мінімуму функції;
• в) екстремуми функції.

Рис. 14.26

Знайдіть проміжки зростання й спадання, точки максимуму і точки мінімуму функції, її максимуми і мінімуми (82—85).

• 1. а); б) ;
• в); г) .
• 2. а); б) ;

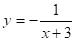
• в); г) .
• 3. а); б) ;
• в); г) .
• 4. а); б) ;
• в); г) .

Знайдіть проміжки зростання й спадання, точки екстремума і екстремуми функції (5−6).

5. а); б) ;

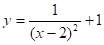
• в); г) .
• 6. а); б) ;
• в); г) .

Дослідження функцій

Побудова графіків функцій.

В школі будували графіки функцій «по точках». У багатьох випадках цей метод дає гарні результати, якщо, звичайно, відзначити досить велике число точок. Однак при цьому приходиться складати великі таблиці значень функції, а головне, можна не помітити істотних особливостей функції й у підсумку помилитися при побудові графіка.

Для того щоб уникнути помилок, треба навчитися виявляти характерні риси функції, тобто попередньо провести її дослідження.

Схема дослідження функцій.

У загальному випадку дослідження передбачає рішення наступних задач:

• 1) Знайти області визначення і значень даної функції f.
• 2) З’ясувати, чи має функція особливости, що полегшують дослідження, тобто чи Є функція f: а) парної чи непарною; б) періодичної.
• 3) Обчислити координати точок перетину графіка з осями координат.
• 4) Знайти проміжки знакосталості функції f.
• 5) З’ясувати, на яких проміжках функція f зростає, а на яких спадає.
• 6) Знайти точки екстремума, вид екстремума (максимум чи мінімум) і обчислити значення f у цих точках.

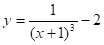
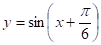
7) Досліджувати поводження функції f в околу характерних точок, що не входять в область визначення (наприклад, точка x = 0 для функції), і при великих (по модулі) значеннях, аргументу.

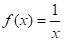
Вертикальні прямі, до яких необмежено наближається графік функції f (наприклад, пряма x = 0 для чи функції прямі для графіка функції, зображеного на рисунку 53), називають вертикальними асимптотами.

Найчастіше графік має вертикальну асимптоту x = a у випадку, якщо вираження, що задає дану функцію, має вид дробу, знаменник якої звертається в нуль у точці a, а чисельник немає. Наприклад, графік функції має вертикальну асимптоту x = 0. Для графіка функції вертикальними асимптотами є прямі, де .

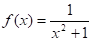
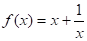
Якщо графік функції необмежено наближається до деякої горизонтальній (у випадку функції це пряма, див. рис. 55) чи похилої (пряма для графіка функції, див. рис. 32) прямої при необмеженому зростанні (по модулі) x, то таку пряму називають горизонтальної (відповідно похилій) асимптотою.