Нескінченно великі змінні величини

Користуючись означенням, можна показати, що сума нескінченно великої величини і величини обмеженої є величина нескінченно велика, тобто. Добуток двох нескінченно великих величин не завжди є нескінченно великою величиною, тому дробовий вираз називають невизначеністю виду. Якщо ж для деякої хоча б однієї послідовності, збіжної до, послідовність границі не має, то функція не має границі в точці… Читати ще >
Нескінченно великі змінні величини (реферат, курсова, диплом, контрольна)
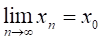
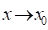
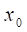
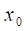
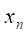
При означенні границізмінної величинивважалось, щозмінюється на деякому скінченому проміжку і що — стале число.
Якщо для довільного >0 існує таке значення, починаючи з якого всі наступні значеннязадовольняють нерівність>, то кажуть, що зміннапрямує до скінченності і пишуть або .
Якщо змінна, то її називають нескінченно змінною величиною.
Користуючись означенням, можна показати, що сума нескінченно великої величини і величини обмеженої є величина нескінченно велика, тобто .
Сума двох нескінченно великих величин одного знака є нескінченно велика, тобто .
Сума двох нескінченно великих величин різних знаків не завжди буде нескінченно великою величиною, тому ця сума називається невизначеністю виду.
Добуток двох нескінченно великих величин не завжди є нескінченно великою величиною, тому дробовий вираз називають невизначеністю виду.
Границя функції в точці
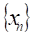
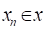
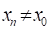
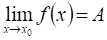
Нехай, функція визначена в деякому околіточки, крім, можливо, самої точки. Число називають границею функції в точці, якщо для довільної збіжної допослідовності, де, , послідовність має границю, яка дорівнює числу, і записують:
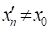
.
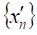
Якщо ж для деякої хоча б однієї послідовності, збіжної до, послідовність границі не має, то функція не має границі в точці.
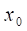
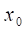
Функція може мати в точцітільки одну границю.