Стійкість і особливість динаміки нелінійних систем

На відміну від лінійних систем стійкість нелінійних систем залежить не тільки від власних параметрів системи, але й від величини зовнішніх дій та місця їх прикладання. Тому не можна говорити про стійкість або нестійкість нелінійної системи взагалі, а можна розглядати стійкість або нестійкість різних режимів роботи системи при різних за величиною діях.

Специфічним динамічним режимом нелінійних систем є режим автоколивань.

Автоколивання — це стійкі незгасаючі періодичні коливання, що виникають у нелінійних системах за умов відсутності зовнішніх періодичних дій. Амплітуда і частота коливань визначаються тільки власними параметрами системи.

Багато особливостей динаміки нелінійних систем можна розглянути на прикладі систем другого порядку, використавши двовимірний простір або площину станів (фазову площину). За координати фазової площини приймають відхилення вихідної величини від її значення, що відповідає усталеному режиму системи, і похідну цього відхилення. Усталеному режиму системи другого порядку відповідає початок координат. Якщо будь-яка дія виводить систему з усталеного режиму, то зображуючи точка рухається у фазовій площині.

Під час перехідного процесу змінюється вихідна величина та її похідна, тому зображуючи точка рухається у фазовій площині по фазовій траєкторії. Початкове положення зображуючої точки відповідає початковим умовам вільного руху системи.

Сукупність фазових траєкторій, що відповідають різним початковим станам системи, називається фазовим портретом. Він дає повне уявлення про динаміку системи.

Динаміка системи другого порядку описується рівнянням:

де нелінійна функція.

Враховуючи, що, рівняння записуємо у вигляді двох рівнянь:

;

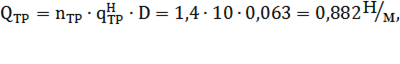
Виключимо з цих рівнянь час, розділивши друге рівняння на перше. Тоді дістанемо рівняння першого порядку:

(*).

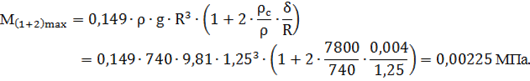
розв’язок якого дає рівняння фазової траєкторії.

Зв’язок між перехідним процесом і фазовою траєкторією проілюструємо на прикладі затухаючого коливального процесу.

Однаковими літерами позначимо точки на графіку перехідного процесу (а) і фазовій траєкторії (б), що відповідають однаковим станам системи. Напрямок руху зображуючої точки при зростанні часу показано стрілкою. Фазові траєкторії мають такі властивості. У верхній напівплощині фазової площини, тому зображаюча точка рухається у бік зростання (зліва направо), у нижній напівплощині, де — у бік зменшення (справа наліво). У точці перетину фазової траєкторії з віссю, тому згідно (*). Звідси випливає, що дотична до фазової траєкторії у точці її перетину з віссю перпендикулярна до цієї осі.

Рівняння (*) однозначно визначає дотичну до фазової траєкторії в усіх точках, крім тих, для яких одночасно виконуються умови:

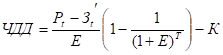
і .

У цих точках, тобто не існує певного напряму дотичної до фазової траєкторії, і з них можуть виходити багато фазових траєкторій. Такі точки називають особливими. В них похідні фазових координат дорівнюють нулю, тому особливі точки є точками рівноваги системи.

Фазові портрети нелінійних систем наведені у таблицях довідникової літератури.

Динамічні процеси у нелінійних системах суттєво відрізняються від процесів у лінійних: значно ширше трактується поняття про стійкість, в тій самій системі залежно від початкових відхилень можуть спостерігатися якісно різні перехідні процеси тощо. В цілому за своїми властивостями нелінійні системи значно багатші за лінійні. Наприклад:

Фазовий портрет, який зображено на рисунку, характеризує динаміку системи, нестійкої у малому (особлива точка — нестійкий фокус). Усталеним режимом цієї системи є автоколивання. Прикладом такої системи може бути система, лінійний аналог якої при малих відхиленнях нестійкий. У цій системі спостерігається розбіжний коливальний процес, проте внаслідок насичення окремих елементів системи амплітуда коливань не зростає нескінченно, а встановлюється на деякому змінному рівні, тобто в системі виникає режим автоколивань. Такому режиму відповідає замкнута траєкторія на фазовій площині.

Ця траєкторія називається стійким граничним циклом. Стійкий граничний цикл становить найважливіший для ТАК тип особливих ліній на фазовій площині. Фазові траєкторії, що починаються всередині й ззовні стійкого граничного циклу, з часом асимптотично наближається до нього.

Якщо фазові траєкторії, близькі до граничного циклу, з часом віддаляються від нього, то граничний цикл буде нестійким.

Приклад фазового портрета з нестійким граничним циклом показано на рисунку.

Він відповідає системі, що стійка у малому і нестійка у великому. Нестійкий граничний цикл визначає межу початкових умов, до якої система зберігає стійкість. Він також становить особливу лінію на фазовій площині.

Дослідження нелінійних систем методом фазової площини

Метод фазової площини належить до таких методів дослідження нелінійних систем. Найповніше цей метод розроблений для систем другого порядку. Сукупність фазових траєкторій (фазовий портрет), що відповідають різним початковим положенням зображуючої точки дає повне уявлення про динаміку нелінійної системи. Тому дослідження нелінійних систем методом фазової площини по суті зводиться до побудови фазового портрета і аналізу за його допомогою динамічних режимів системи.

Як зазначалось раніше, рівняння фазової траєкторії є розв’язком рівняння.

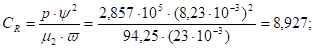
першого порядку. (*).

Спосіб розв’язування цього рівняння залежить від типу характеристики нелінійної ланки. Загальним методом розв’язання є чисельне інтегрування за допомогою ЕОМ. Для кусково-лінійних нелінійних характеристик у деяких випадках розв’язок рівняння першого порядку може бути знайдено аналітично для окремих лінійних ділянок нелінійної характеристики. Кожна лінійна ділянка нелінійної характеристики описується своїм рівнянням вигляду (*), отже буде багато різних рівнянь фазових траєкторій. При цьому на фазовому портреті з’являються так звані лінії перемикання, що розділять фазову площину на зони з різними фазовими траєкторіями.

Якщо нелінійну систему зведено до найпростішої і розглядається вільний рух системи, то рівняння ліній перемикання визначається безпосередньо за математичним описанням нелінійної ланки.

Якщо на фазовій площині є лінії перемикання, то при розрахунку фазових траєкторій початкові значення та кожної ділянки визначаються через їх кінцеві значення на попередній ділянці.

Фазові траєкторії можна побудувати й не розв’язуючи рівняння (*), якщо скористатися методом ізоклін. Ізокліни (лінії однакового нахилу) — це лінії, вздовж яких похідна має стале значення. Через те, що ізокліна становить геометричне місце точок з однаковим кутом нахилу дотичних до фазових траєкторій, що проходять через ці точки. Кут нахилу дотичних до осі абсцис визначається із співвідношення.

Рівняння ізоклін знаходять з рівняння (*), якщо прийняти, тобто.

.

Це рівняння є алгебраїчним. Надаючи С різних значень від до, побудуємо сім'ю ізоклін, використавши яку, легко дістати фазові траєкторії при будь-яких початкових умовах (будь-якому початковому положенні зображуючої точки). Сім'ю ізоклін покажемо графічно:

Стрілками на ізокліні показано кути нахилу дотичних до фазових траєкторій. Для побудови фазової траєкторії слід задати початкові умови через точку провести дві лінії. Нахил першої має збігатися з нахилом стрілки на ізокліні, другої - з нахилом, що відповідає суміжній ізокліні. Вважаємо, що точка лежить на середині відрізка, що відтинається на ізокліні лініями, проведеними з точки. Аналогічно відшукуються всі інші точки і будується фазова траєкторія.

За фазовим портретом нелінійної системи можна зробити не тільки якісну оцінку її динаміки, а й визначити кількісні показники якості перехідних процесів.

За граничним циклом на фазовому портреті можна визначити амплітуду і частоту автоколивань. Якщо граничний цикл наближено замінити еквівалентним еліпсом з півосями і, то параметри автоколивань можна визначити за такими формулами:

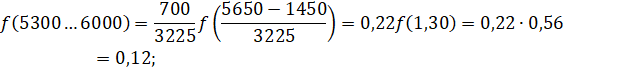
— амплітуда; - частота; - період;

Метод гармонічної лінеаризації

Метод гармонічної лінеаризації є принципово наближеним методом. Ідею цього методу було запропоновано М. М. Криловим і М. М. Боголюбовим у 1934р.

Метод гармонічної лінеаризації використовується для дослідження автоколивань у нелінійних системах високого порядку, а також для оцінки якості перехідних процесів.

Для пояснення суті гармонічної лінеаризації розглянемо походження гармонічного сигналу.

(1) через нелінійну ланку.

На виході нелінійної ланки в загальному випадку створюється періодичний сигнал.

.

Який можна розкласти в ряд Фур'є:

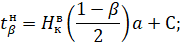
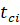
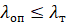
Прийнявши що справедливо для нелінійних характеристик, симетричних відносно початку координат, вираз (1) запишемо у вигляді:

вищі гармоніки (2).

Якщо врахувати, що з (1) випливає.

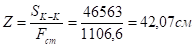
то вираз (2) можна записати у вигляді:

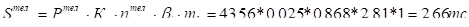
вищі гармоніки, або.

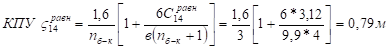
вищі гармоніки,.

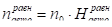
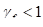
де; - коефіцієнти гармонічної лінеаризації. Ці коефіцієнти згідно з виразом (3) і (4) є функціями амплітуди .

Отже, нелінійна функція при замінюється виразом (5), який з точністю до вищих гармонік є лінійним. Ця операція називається гармонічною лінеаризацією.

Гармонічна лінеаризація по суті є наближеною. Вона ґрунтується на таких припущеннях:

• 1. У системі існують автоколивання;
• 2. Коливання на вході нелінійної ланки є синусоїдальними, тобто лінійна частина системи виконує функції фільтра основної гармоніки; це припущення прийнято називати гіпотезою фільтра.

Гармонічна лінеаризація дає можливість описувати нелінійні ланки лінійними рівняннями. Якщо виконується гармонічна лінеаризація, нелінійна характеристика замінюється прямою лінією з коефіцієнтом нахилу, величина якого залежить від амплітуди вхідного сигналу.

Так, з графіка залежності видно, що при коефіцієнт і лінеаризувала характеристика збігається з лінійною частиною характеристики ланки з насиченням (характеристика 1).

При зростанні амплітуди коефіцієнт зменшується і лінеаризувала характеристика набуває вигляду характеристик (2), (3) і т. д. при коефіцієнт прямує до нуля. Це пояснюється тим, що при зростанні амплітуди вхідного сигналу амплітуда вихідного сигналу внаслідок насичення залишається незмінною, тобто коефіцієнт передачі ланки безперервно зменшується.

Отже, гармонічна лінеаргуація замінює нелінійну ланку не на звичайну лінійну ланку, а на ланку, коефіцієнт передачі якої є функцією амплітуди (а в загальному випадку й частоти) вихідного сигналу.

Тільки для режиму автоколивань, коли (А і щ — відповідно амплітуди і частоти автоколивань), коефіцієнти гармонічної лінеаризації є сталими величинами.