Конструкція для х і у

Будь-яке просте р виду 4k+1 однозначно подається як; математики намагалися знайти вирази для х і у в термінах р, оскільки конструкція зазвичай приносить більше задоволення, чим чистий доказ існування, хоча межа між ними не завжди виразно проводиться. Відомі чотири конструкції для х і у, вони належать Лежандру (1808), Гаусу (1825), Серре (1848) і Якобшталю (1906); ми викладемо їх, не входивши в деталі доказів. Представляє інтерес різноманітність методів, використовуваних в цих конструкціях.

Конструкція Лежандра заснована на розкладанні в безперервний дріб. Період складається з симетричних частин за якими слідує. В такій формі це застосовано не лише до простого виду 4k+1, але і до будь-якого числа, що не є точним квадратом. Нагадаємо, що якщо в симетричній частині немає центрального члена, то вирішуване рівняння Вірне і зворотне, хоча це і не було доведено. Лежандр абсолютно елементарним способом довів, що якщо р — просте виду 4k+1, то рівняння має розв’язки. Отже, в силу тільки що сформульованої зворотної теореми центральний елемент в розкладанні відсутній і період має вигляд Нехай тепер б — повна частка, що починається в середині періоду, саме:

Це чисто періодичний безперервний дріб, період, який складається з. Оскільки цей період симетричний, ми маємо де означає число, зв’язане з. Представимо тепер у виді.

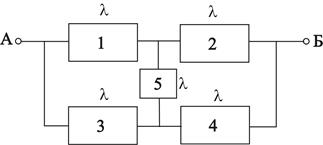
з цілими Р і Q. Рівняння дає.

або.

Це конструкція Лежандра. Як приклад розглянемо випадок р = 29. Розкладання в безперервний дріб протікає так:

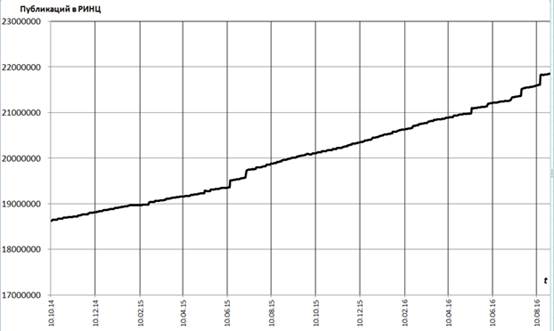
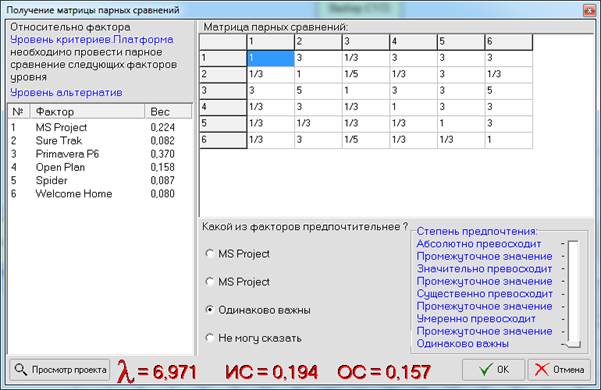
Безперервний дріб для тому рівна Потрібна нам повна частка — число, звідси Р = 2 і Q = 5, і.

Друга конструкція була запропонована Гаусом; за формою ця конструкція найбільш проста (хоча обгрунтувати її і не так просто). Якщо р = 4k + 1, покладемо.

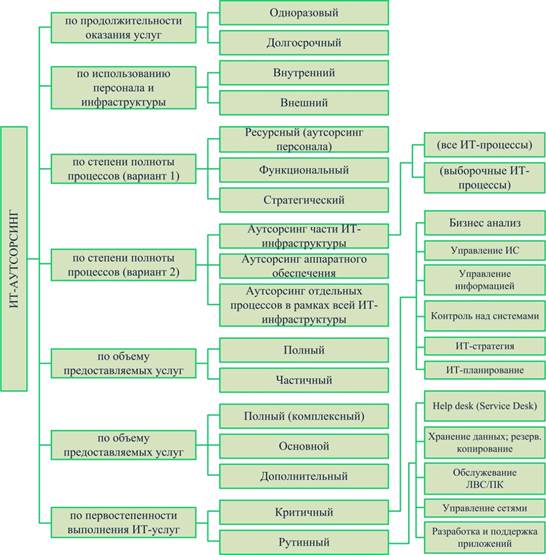
де х і у вибрані між Тоді Доказ був даний Кошs і Якобшталем, обидва докази не дуже прості. Щоб проілюструвати конструкцію, покладемо знову р = 29. Тоді.

Ця конструкція, незважаючи на свою елементарність, не дуже зручна для обчислень.

Третя конструкція — конструкція Серре. Вона, подібно до побудови Лежандра, використовує безперервні дроби, але тут розкладається в безперервний дріб раціональне число. Розкладемо в безперервний дріб (h задовольняє рівнянню і. Можна довести, що цей безперервний дріб має вигляд.

(8).

отже послідовність елементів безперервного дробу симетрична і центральний член відсутній. Покладемо.

Тоді.

Наприклад, якщо р = 29, то h = 12, оскільки.

Безперервний дріб Звідси.

Та ж побудова в декілька іншій формі було запропоновано в 1855 році Смітом. Він хотів дати простий і безпосередній доказ того, що всяке просте число виду +1 подається як сума двох квадратів. Не користуючись рівняннями, Сміт довів, що існує таке h, що і безперервний дріб має вигляд (8). Визначаючи х і у, як і раніше, він довів, наслідуючи Серре, що.

Перейдемо тепер до конструкції Якобшталя (Jacobsthal). Розглянемо наступну суму символів Лежандра :

де, а — яке-небудь число, не порівнянне з 0 по mod р, а підсумовування поширюється на деяку повну систему вирахувань, наприклад на числа. Легко довести, що має лише два можливі значення: одне, коли, а — квадратичне вирахування, інше, коли, а — квадратичне невирахування. Більше того, обидва ці значення парні, бо доданок з n = 0 дорівнює 0, а складові, відповідні n іп, однакові, оскільки. Покладемо.

де R — яке-небудь квадратичне вирахування, a N — якесь квадратичне невирахування. Тоді.

Доказ цього досить простий.

Як приклад візьмемо знову р = 29. Покладемо R = 1, а N=2 (2 квадратичне невирахування по модулю 29). Значення по складаються з 0 і чисел.

кожне з яких зустрічається двічі. Сума відповідних їм символів Лежандра дорівнює 5, так що х = 5. Значення по складаються з 0 і чисел узятих по два рази кожне. Сума значень їх символів Лежандра дорівнює 2, звідки у = 2.