Кореляційна довжина. 
Поріг протікання електричного струму в тонких металевих плівках

Найбільш важливою кількісною перколяційної характеристикою з практичної точки зору є кореляційна довжина е, яка, грубо кажучи, є середнім розміром перколяційних кластерів разом з типовим розміром великих незайнятих ділянок поблизу неперервного кластера вище порогу протікання p_c. Як тільки поріг перколяції буде перетнуто, то великі кластери почнуть приєднуватись один до одного та ставати все більшими і більшими і, як наслідок кореляційна довжина почне змінюватись за законом.

е~|p-p_c|^-н (1).

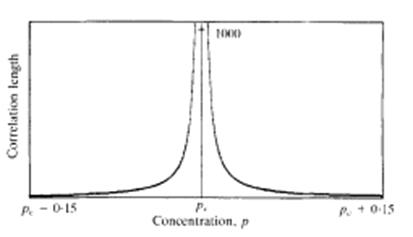
Рис. 5. Залежність кореляційної довжини від концентрації

тут (для двовимірних ґраток рівна 4/3) є прикладом критичного перколяційного вказівника. Більшість важливих перколяційних величин (таких, як густина неперервного кластера, середній розмір кластерів, провідність випадкових перколяційних резистивних мереж та ін.) ведуть себе поряд із p_c за деяким степеневим законом (на рис. 2, при p < p_c густина неперервного кластера і провідність випадкової перколяційної резистивної мережі є величинами (p-p_c)^5/36 та (p-p_c)^1/3 відповідно). Відповідні критичні індекси були встановлені і всесторонньо вивчені, між ними була встановлена залежність. 8].

Якщо розглядати неперервний кластер із великої відстані (тобто, з відстані при якій ми не зможемо відрізнити будь-які деталі, окрім найбільшої неоднорідності е), то буде здаватись, що ми маємо однорідну структуру. Якщо підійти до цього більш уважно, так, щоб можна було розрізняти частинки менші від е, то можна побачити, що неперервний кластер є самоподібним. Явище самоподібності поширилось з появою фрактальної геометрії (Мандельброт 1982) і значить, що самоподібні об'єкти складаються з однакових структур з різними кореляційними довжинами, або, іншими словами, якщо дивитись на фотографії цього кластера при різних збільшеннях ми не в змозі визначити, в якому порядку ці картини були зроблені.

Кореляційна довжина як єдина, що відповідає «макроскопічній» довжині, також визначає ефективну розмірність перколяційного об'єкта: наприклад, тонкі плівки, що розглядаються в цій роботі, насправді складаються не з двовимірних зерен. Тим не менше, поблизу порога протікання їх можна вважати двовимірними, тому що можна вважати, що кореляційна довжина прямує до безмежності і стає набагато більшою від товщини плівки.

Якщо порівняти кореляційну довжину з характерною довжиною l для фізичної величини при вивченні певних властивостей (наприклад, довжина хвилі світла при вивченні оптичних властивостей), то можна виділити два режими:

• 1. В однорідному режимі () об'єкт є ефективно однорідним для і детальна структура протікання в перколяційний мережі не має значення для дослідження властивостей.
• 2. В неоднорідному режимі () топологія перколяційної мережі має прямий вплив на властивості об'єкта, що вивчається. Рівняння (1) свідчить про те, що неоднорідний режим завжди може бути досягнутим поблизу порогу перколяції.

В якості першого прикладу в даному розділі, можна навести деякі результати останніх досліджень оптичних властивостей неоднорідних плівок металу поблизу p_c. Оптичні властивості суміші метал-діелектрик були традиційно вивчені в модифікованій теорії ефективного середовища (Ландауер 1978), основними припущеннями якої є:

• 1. Розмір металевих зерен є значно меншим, аніж оптична довжина хвилі л;
• 2. Форма металевих зерен є визначена (наприклад, еліпсоїдальна)

Жодне із цих тверджень не виконується поблизу p_c, де кластери великої неправильної форми і структури можуть виростати до макроскопічних розмірів. Ефективне середнє наближення добре працює в однорідному режимі (), але не виконується в напівнеперервних плівках в неоднорідному режимі (). [6].

Деякі групи експериментаторів досліджували пропускання і відбивання напівнеперервних металевих плівок (Au, Al: Ягіл та Дойчер 1987, Au: Гаденн та інші 1987, Al: Кунц та інші) в інфрачервоному спектральному діапазоні (л > 1~5 мкм), де оптичні властивості регулюються вільними електронами металу і, можливо тому, корелюють з постійними електричними властивостями (які добре відомі з дослідження структури плівок). Основні висновки з цих робіт можна описати так (Гаденн та інші):

• 1. Поведінка коефіцієнта відбивання та пропускання поблизу порога перколяції, здається універсальною та дуже схожою для різних плівок (для прикладу, плівки з різними розмірами зерен).
• 2. Близько до p_c, відбивання і пропускання слабо залежать від довжини хвилі і їх поведінка близька до лінійної.
• 3. Дуже велике поглинання (? 40%) в окрузі p_c не залежить від довжини хвилі

Ягіл та Дойчер (1988) запропонували просту феноменологічну теорію, основану на самоподібності металевої сітки в напівнеперервному режимі і змогли пояснити явища 1 та 2. Тепер спробуємо пояснити суть їх розрахунків для пропускання в напівнеперервних металевих плівок.

Основним кроком до розрахунків є вимірювання кореляційної довжини на основі деякої ідеї реально-просторової перенормовувальної техніки (Вілсон 1979, Шауффер 1985). Метод перенормування полягає в розбитті вузлів ґратки в клітинки лінійних розмірів з певної константою розміру (як правило, менших від кореляційної довжини) і заміною ними так званих «супер-ділянок». Концентрація заповнених місць р, кажучи в загальному, змінилась (з концентрацією окупованих супер-ділянки р') в результаті «усереднення» процес-ділянками, в яких більшість місць є зайнятими «супер-ділянками» (після перенормування утворень з більшістю незайнятих місць). Тим не менше при p=p_c перколяційна мережа є напівпровідною і тому р не змінюється.

Якщо ми вивчаємо напівнеперервні тонкі металеві плівки, то характеристична мікроскопічна довжина а є типовим розміром металевих зерен. Світлова хвиля з довжиною хвилі л «бачить» зразки і переформовує їх по довжині л (або л/2р (обернене до оптичного хвильового числа)). Ділянки, які є окупованими під час цього починають поводити себе як металеві. Відносна кількість «металевих» (р') і «діелектричних» (1- р') ділянок на розмірності л/2р легко визначається: кореляційна довжина може бути виражена двома просторовими масштабами, такими як а та л/2р, тому.

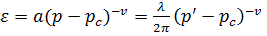
(2).

(слід відзначити, що p_c не повинно змінюватись) і також.

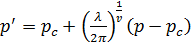
(3).

Подальше перенормування масштабу та загального пропускання Т плівки може бути розраховане як сума пропускання в ділянках з характерними величинами л/2р, в яких є як і металеве пропускання (Т_m) та і діелектричне (Ti):

(4).

З рівняння (3) ми отримуємо:

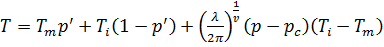
(5).

Рівняння (5) передбачає лінійну залежність пропускання від р і довжина хвилі випромінювання і незалежність при p=p_c (рис. 6).

Спостереження (3) було пояснено Робіном і Соуіллардом (1989), які приймали до уваги детальні знання про внутрішню структуру кластерів поблизу перколяційного порогу. 4].

Поведінка напівнеперервних надпровідних плівок або випадкових надпровідних-ненадпровідних сумішей, а також частотна залежність провідності тонких металевих плівок слугують додатковими прикладами відмінностей між однорідними і неоднорідними структурами.

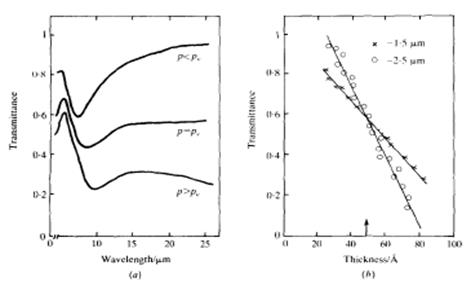
Рис. 6. Пропускання тонких плівок золота в вигляді функції довжини падаючого світла (а) та товщини плівки (б). Хрестики та круги (на б) відповідають довжинам хвиль 1,05 мкм та 2,5 мкм, відповідно. Стрілка на рис. б) відмічає поріг протікання (перколяційний поріг, критична товщина плівки), при якому коефіцієнт пропускання стає незалежним від довжини хвилі.