Вектори та тензори. Їх перетворення при поворотах системи координат

Пусть и две декартовы системы координат, повернутые друг относительно друга, с базисными векторами (ортами), , образующими правые ортонормированные тройки. Поскольку системы координат и декартовы, то и .

Здесь — символ Кронекера.

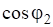
Произвольный вектор можно разложить подобно радиус-вектору по ортам обеих систем координат:

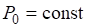
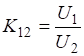
(Данные выражения записаны с использованием правила Эйнштейна, которое подразумевает суммирование по парам повторяющихся индексов, в то время как знак суммы опускается. Это правило будет использовано в дальнейшем).

Величины и называются компонентами вектора и являются ортогональными проекциями данного вектора на орты и :

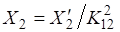
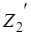
и .

Установим связь между проекциями вектора на различные базисные орты:

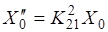
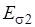
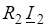
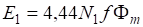
где — матричные элементы матрицы поворота. Если объединить компоненты в одностолбцовую матрицу, а компоненты в одностолбцовую матрицу, то закон преобразования компонент вектора можно записать в матричных обозначениях:

Задание. Убедиться в справедливости последнего равенства, раскрыв в явном виде произведение матриц.

Докажем, что матрица ортогональна, т. е. :

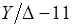
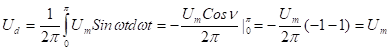
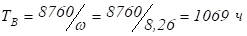
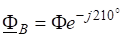
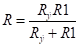
При выводе мы воспользовались свойствами скалярного произведения и тем, что, поскольку левая часть равенства представляет собой разложение базисного орта по базисным ортам .

Задание. Докажите, что.

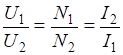
С учетом закона преобразования компонент вектора при повороте системы координат можно дать следующее определение вектора:

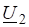
Вектором называется трехкомпонентная величина, компоненты которой преобразуются при повороте системы координат так же, как компоненты радиус-вектора по правилу (2.1) с помощью матрицы поворота .

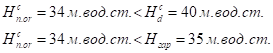
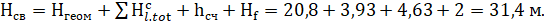
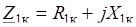
Такое определение вектора допускает обобщение на случай величин с числом компонент, большим трех. Так возможны девятикомпонентные величины, компоненты которых нумеруются двумя векторными индексами, каждый из которых пробегает независимо значения 1,2,3. Возможны 27-и компонентные величины, компоненты которых нумеруются тремя векторными индексами. Наконец, возможны — компонентные величины, компоненты которых нумеруются N векторными индексами (векторные индексы независимо пробегают множество значений 1,2,3). Если компоненты этих многокомпонентных величин преобразуются по законам:

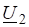
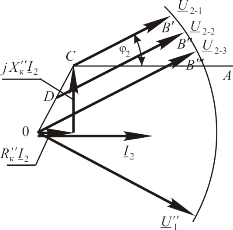
то эти многокомпонентные величины называются тензорами соответственно второго, третьего и N-ранга. Ранг тензора определяется числом векторных индексов, нумерующих его компоненты. Максимальное число независимых компонент тензора ранга N равно в случае трехмерного пространства.

Вопрос. Чему равно число независимых компонент тензора ранга N в случае двумерного пространства?

Компоненты тензора второго ранга естественно объединяются в квадратную матрицу со следующим законом преобразования матричных элементов:

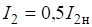
или ,.

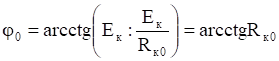
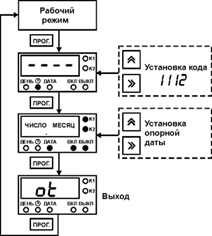
где и квадратные матрицы с матричными элементами и .

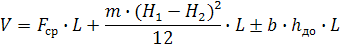
Очевидно, что вектор является тензором первого ранга, а скаляр — нулевого. Ранг тензора также называют тензорной размерностью, или валентностью.

Задачи

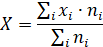
2.1 Найти матрицу преобразования системы декартовых координат на плоскости при повороте на угол .

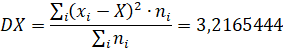
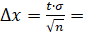
Решение задачи 2.1 Матричные элементы искомой матрицы вычисляются как скалярные произведения, здесь индексы i, j принимают только два значения: 1 или 2. Так как все орты по определению имеют единичные модули, каждое скалярное произведение равно косинусу угла между соответствующими ортами. Нарисуйте на листе бумаги пояснительный чертеж и убедитесь, что углы между парами базисных орт и одинаковы и равны углу поворота. Поэтому. Угол между ортами равен, и соответственно. Угол между ортами равен, поэтому .

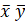
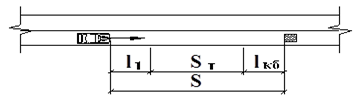
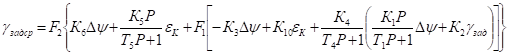
2.1.1. Убедиться, что определитель матрицы равен 1.

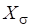
2.1.2 Убедиться, что матрица ортогональна, т. е., гдетранспонированная матрица, аединичная матрица.

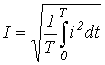
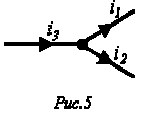
2.1.3 Убедиться, что — матрица поворота на угол совпадает с произведением матриц и, которые являются матрицами поворота на углы и соответственно.

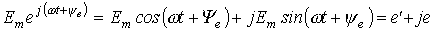
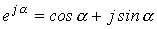
2.1.4. Убедиться, что матрица поворота на угол совпадает с матрицей, где — матрица поворота на угол .

• 2.2 Найти матрицу поворота в трехмерном пространстве относительно заданной координатной оси на угол .
• 2.2.1 Вокруг оси Oz

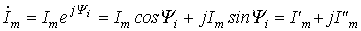
Решение задачи 2.2.1 Очевидно, что базисные орты, повернутой вокруг оси Oz системы координат, лежат в Oxy плоскости исходной координатной системы. Выше (см. задачу 2.1) мы уже вычислили скалярные произведения для i, j=1 и 2. Фактически мы нашли соответствующие им матричные элементы искомой матрицы повороты в трехмерном пространстве:,. Для нахождения остальных матричных элементов заметим, что базисные орты ортогональны орту, поэтому. После выполнения поворота вокруг оси Oz направление аналогичной оси новой системы координат не изменится, т. е. орт. Оставшиеся матричные элементы вычисляются тривиально: (j=1,2,3). Выпишем явный вид матрицы поворота вокруг оси Oz:

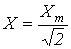
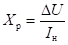
2.2.2 Вокруг оси Ox.

Решение задачи 2.2.2 во многом аналогично решению предыдущей задачи.

Приведем в качестве ответа явный вид искомой матрицы поворота:

2.2.3 Вокруг оси Oy.

2.3 Найти матрицу поворота в трехмерном пространстве на углы Эйлера. Углы Эйлера определены следующим образом: вначале проводится поворот на угол вокруг оси, затем производится поворот на угол вокруг новой оси, а после этого производится поворот на угол вокруг новой оси .

2.3.1 Доказать, что матрица может быть записана в виде произведения трех матриц, где матрица соответствует повороту на угол вокруг оси, матрица соответствует повороту на угол вокруг новой оси, матрица соответствует повороту на угол вокруг новой оси .

Решение задачи 2.3.1 Рассмотрим вектор с компонентами, заданными в исходной системе координат. Объединим его компоненты в матрицу, состоящую из одного столбца (в так называемый вектор-столбец). Компоненты этого вектора в новой системе координат, повернутой вокруг оси на угол, вычислим как матричное произведение. Давайте рассматривать повернутую систему координат как новую исходную, и совершим далее поворот вокруг ее оси на угол. Компоненты вектора в новой, повернутой системе координат вычислим как матричное произведение .

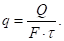
Матрица поворота составлена из косинусов углов между ортами новой исходной, и новой повернутой координатных систем. Для ее вычисления мы фактически должны повторить решение задачи 2.2.2 и получить в результате ту же матрицу с заменой угла на. Давайте примем систему координат.

за новую исходную, и выполним последний поворот вокруг оси на угол. Компоненты вектора в системе координат теперь вычисляются как .

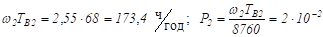
Матрица составлена их косинусов углов между соответствующими ортами. Она совпадает с матрицей поворота вокруг оси Oz, найденной в ходе решения задачи 2.2.1, с заменой угла на. Итого:. Приведем для справки явный вид матрицы поворота на углы Эйлера, , .

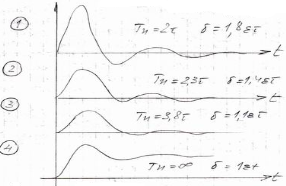
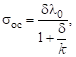
• 2.3.2 Доказать, что .
• 2.3.3 Выразить матрицу обратного преобразования через произведение матриц поворотов вокруг осей Ox и Oz.
• 2.4 Найти матрицу для следующих углов Эйлера:
• 2.4.1

2.4.2.

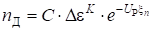
2.4.3.

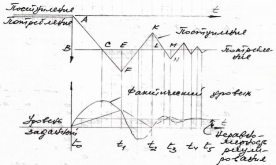
2.4.4.

2.4.5.

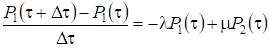
2.4.6.

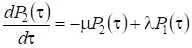
• 2.5 В случае двумерного пространства вычислить компоненты вектора в системе координат повернутой на угол по сравнению с исходной. Компоненты вектора и угол следующие:
• 2.5.1

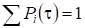
2.5.2.

2.5.3.

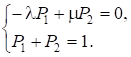
2.5.4.

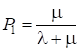
2.5.5.

2.5.6.

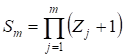
• 2.6 В случае двумерного пространства вычислить компоненты тензора второго ранга в системе координат, повернутой на угол по сравнению с исходной. Компоненты тензора и угол следующие:
• 2.6.1

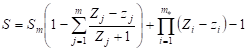
2.6.2.

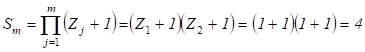
2.6.3.

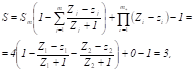
2.6.4.

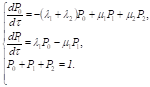
2.6.5.

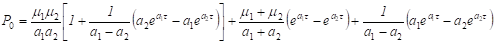
2.6.6.

• 2.7 В трехмерном пространстве заданы компоненты вектора. Найти компоненты вектора в системе координат, повернутой на угол вокруг оси Ox по сравнению с исходной. Компоненты вектора и угол следующие:
• 2.7.1

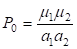
2.7.2.

Решение задачи 2.7 дается общей формулой:

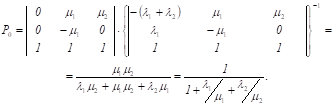
Для конкретного варианта, указанного в пункте 2.7.1 получаем.

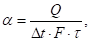
• 2.8 В трехмерном пространстве заданы компоненты вектора. Найти компоненты вектора в системе координат, повернутой на угол вокруг оси Oy по сравнению с исходной. Компоненты вектора и угол следующие:
• 2.8.1

2.8.2.

• 2.9 В трехмерном пространстве заданы компоненты вектора. Найти компоненты вектора в системе координат, повернутой на угол вокруг оси Oz по сравнению с исходной. Компоненты вектора и угол следующие:
• 2.9.1

2.9.2.

2.10 В случае двумерного пространства найти компоненты тензора в системе координат, повернутой относительно исходной на угол .