Асимптотичне дослідження раціональних функцій і побудова їх графіків за допомогою прямолінійних асимптот

Побудову графіка зазвичай починають з асимптотного дослідження функції, тобто пошуку асимптот. При дослідженні поведінки функції на нескінченних гілках (тобто при і) і поблизу точок розриву часто виявляється, що графік функції як завгодно близько наближається до тієї чи іншої прямої. Такі прямі називають асимптотами. Нагадаємо означення асимптоти. «Асимптотою графіка функції називають пряму, що володіє наступною властивістю: відстань від точки до цієї прямої прямує до нуля при русі цієї точки до нескінченності уздовж гілки графіка».

Мене зацікавило питання: «Чи не можна з першого погляду визначити, які асимптоти має графік і скільки їх?».

Приклад № 1.

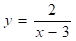
Досліджуємо функцію (рис. 1).

• 1. :;
• 2. — функція загального виду, неперіодична;
• 3. Функція невизначена в точці (саме ця точка визначає вертикальні асимптоти);
• 4. Дріб не може бути рівний нулю, так як чисельник дорівнює 2, тобто (отже горизонтальна асимптота).

Асимптотичне дослідження функції показує: що графік має вертикальну асимптоту х = 3, так як при і; горизонтальну асимптоту, причому ця пряма є асимптотою для обох віток графіка, так як як при, так і при .

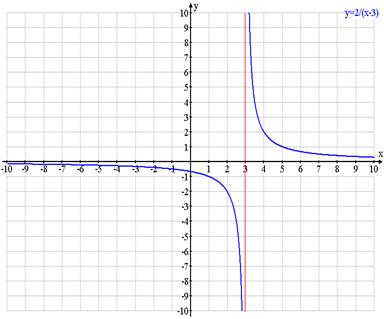
Рис. 1.

Висновок: вертикальні асимптоти проходять через точки розриву досліджуваної функції, якщо функція задана раціональним виразом, то найчастіше одразу видно, є вона неперервною чи ні, оскільки зазвичай буває неважко визначити, при яких значеннях аргументу дріб дорівнює.

Приклад № 2.

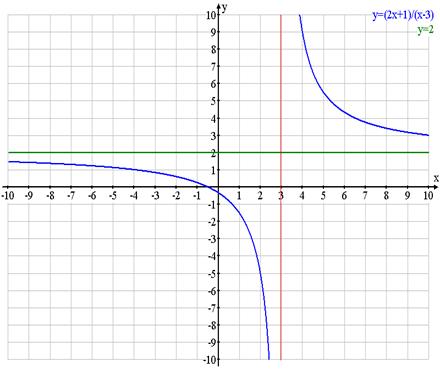
Рис. 2.

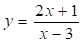
Досліджуємо функцію (рис. 2). Для того, щоб провести асимптотичне дослідження функції, треба виділити «цілу частину» дробу, поділивши чисельник на знаменник. Ми одержимо .

Тепер досліджуємо:

• 1. :;
• 2. — функція загального виду, неперіодична;
• 3. Функція невизначена в точці ;

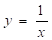
Зараз видно, що графік цієї функції виходить з графіка наступними перетвореннями: зміщенням на 3 одиниці вправо, розтягуванням в 7 разів уздовж осі Оу і зміщенням на 2 одиниці вгору.

Асимптотичне дослідження функції показує: що графік має вертикальну асимптоту х = 3, так як при і; горизонтальну асимптоту, причому ця пряма є асимптотою для обох віток графіку, так як як при, так і при .

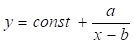
Висновок: якщо при діленні чисельника на знаменник виходить остача а,, то графік цієї функції має дві асимптоти: вертикальну x = в та горизонтальну y = .

Приклад № 3.

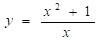
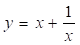
Досліджуємо функцію. Перетворимо функцію до виду. Другий вираз зручніше з точки зору асимптотичного дослідження.

• 1. :;
• 2. — функція загального виду, непарна;
• 3. Функція невизначена в точці (саме вона визначає вертикальні асимптоти);
• 4. Дріб не може бути рівний нулю.

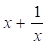
Далі при дослідженні я звернула увагу, що, вирази і задають одну й ту ж функцію, другий вираз — результат ділення чисельника на знаменник. Але другий вираз зручніше з точки зору асимптотичного дослідження. Замислилась. Виділена ціла частина являє собою пряму, отже, отриманий вираз підказує нам, що при значення нашої функції прямують до значень прямої. Значить є похилою асимптотою.

Мої дослідження привели мене до наступного припущення: похилу асимптоту можна легко знайти, розділивши чисельник раціонального виразу, яким задана функція, на його знаменник. Дослідивши графіки раціональних функцій, я прийшла до наступного висновку:

• 1. Якщо при діленні чисельника на знаменник виходить остача, то графік має горизонтальну асимптоту, рівну .
• 2. Якщо показник степеня чисельника (позначим його через) меньше показника степеня знаменника (позначим його через), то графік має горизонтальну асимптоту .
• 3. Якщо показник степеня чисельника дорівнює показнику степеня знаменника, то графік має горизонтальну асимптоту .

Потім я почала досліджувати раціональні функції з більш складними виразами, такими, у яких показник степеня чисельника на одиницю більше від показника степеня знаменника, тобто .

Досліджуємо функцію показник степеня чисельника більше показника степеня знаменника на 1, тобто.

Приклад № 4.

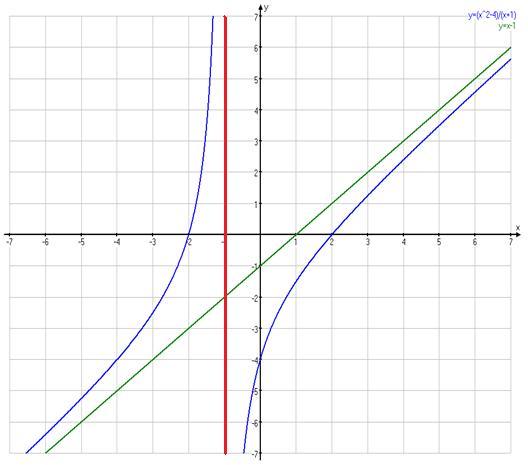
Рис. 4.

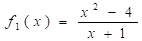
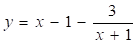
Досліджуємо функцію (рис. 4), та, уявімо її у вигляді.

• 1. :;
• 2. — функція загального виду, неперіодична;
• 3. Функція невизначена в точці ;

За асимптотичним дослідом ми бачимо, що вона має вертикальну асимптоту не має горизонтальних асимптот, в ролі асимптоти виступає пряма, яка є похилою асимптотою.

Приклад № 5.

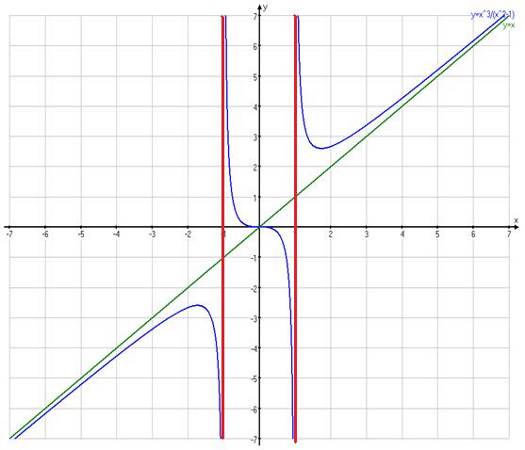
Рис. 5.

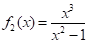
Досліджуємо функцію (рис. 5), яку можно представити у вигляді.

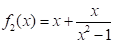
• 1. :;
• 2. — функція непарна, неперіодична;
• 3. Функція невизначена в точках, ;

Асимптотичне дослідження функції показує, що графік не має горизонтальних асимптот, має дві вертикальні асимптоти і, й одну похилу .

Зі своїх досліджень я зробила наступний висновок: якщо, то графік функції має похилу асимптоту, тобто таку пряму, котора задаеться рівнянням де й.