Принцип кінетостатики.
Кінетостатичний аналіз механізмів

Момент інерції — це аналог маси при обертальному русі. Маса — це міра інертності тіла при поступальному русі. Де — тангенціальне прискорення, м/с2; — довжина ланки, м. Де — маса ланки, кг; — прискорення центра мас ланки, м/с2. Визначаємо плече (це перпендикуляр із т. K на вектор): Ураховується також головний момент сил інерції, Нм: Згадаємо спочатку поняття маси і моменту інерції. Визначаємо… Читати ще >
Принцип кінетостатики. Кінетостатичний аналіз механізмів (реферат, курсова, диплом, контрольна)
Принцип кінетостатики полягає в тому, що в число зовнішніх сил, що діють на ланки механізму, запроваджують сили інерції, які є фіктивними для самої ланки, але реальними для її зв’язків.
Принцип кінетостатики ґрунтується на відомому положенні Д’Аламбера, згідно з яким система сил, до якої уведені сили інерції, вважається рівноважною, і для неї придатні рівняння статики.
Отже, при включенні в число сил, що діють на ланку, сили інерції, ланка умовно вважається у стані спокою, тому можна застосовувати рівняння статики.
Цей принцип є методологічним.
Урахування сил інерції
Плоско паралельний рух ланки
Згадаємо спочатку поняття маси і моменту інерції.
Маса — це міра інертності тіла при поступальному русі.
Момент інерції — це аналог маси при обертальному русі.
Зв’язок між масою і моментом інерції:
де — маса, кг; - радіус інерції, м.
Розглянемо ланку ВС, яка здійснює плоскопаралельний рух (рис. 5.4,а) та її план прискорень (рис. 5.4,б).
Елементарна сила інерції для матеріальної точки визначається за формулою:
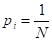
(5.5).
де — елементарна маса; - прискорення матеріальної точки.
а. — ланка, що здійснює плоскопаралельний рух;
б. — план прискорень ланки Виділяємо на ланці ВС (рис. 5.4,а) матеріальну точку D, тоді для неї:
.
Аналогічно для матеріальної точки К:
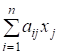
.
Але ланка — це система матеріальних точок, отже, для ланки маємо головний вектор сил інерції, Н:
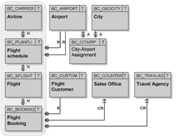
(5.6).
де — маса ланки, кг; - прискорення центра мас ланки, м/с2.
Ураховується також головний момент сил інерції, Нм:
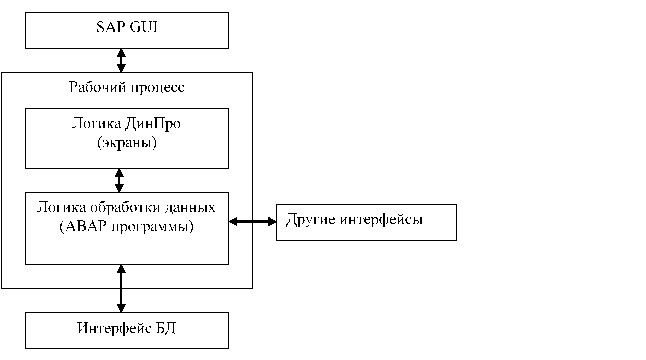
(5.7).
де — момент інерції, кгм2; - кутове прискорення ланки, с-2.

(5.8).

де — тангенціальне прискорення, м/с2; - довжина ланки, м.
Для спрощення розрахунків головний вектор і головний момент сил інерції замінюються результуючою силою, плече якої h дорівнює (рис. 5.5):

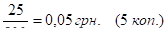
або в масштабі:. (5.9).
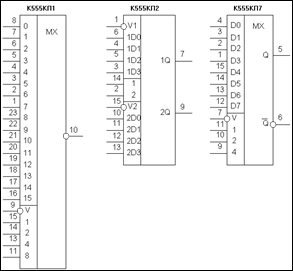
Рис. 5.5. Прикладання результуючої сили інерції
Із центра мас ланки S проводимо коло радіусом, результуюча сила прикладається по дотичній до цього кола, паралельно та протилежно (s), і утворює момент проти (рис. 5.5).
Поступальний рух ланки
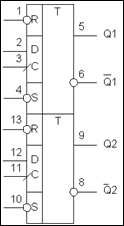
При поступальному русі ланки враховується тільки головний вектор сил інерції, а головний момент сил інерції, т. щ. (рис. 5.6).

1.4.3 Обертальний рух ланки навколо центральної осі
При обертальному русі навколо центральної осі враховується тільки головний момент сил інерції, а головний вектор сил інерції, т. щ. (рис. 5.7).
1.4.4 Обертальний рух відносно довільної осі
До ланки ОА прикладені головний вектор і головний момент сил інерції (рис. 5.8).
Переносимо вектор в довільну точку K, одразу прикладаючи протилежно йому той же вектор .
Рис. 5.8. Урахування сил інерції при обертальному русі відносно довільної осі
Визначаємо плече (це перпендикуляр із т. K на вектор):
.
Визначаємо відстань SK, розглядаючи трикутник KSN:
Отже,.
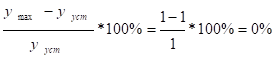
(5.10).
де — радіус інерції, м.
Точка K називається центром хитання ланки.