Завдання 4. Обчислення ймовірностей подій

Умови: Ймовірність появи випадкової події в кожній із 400 незалежних експериментів є величиною сталою і = р. Розв’язок: Оцінимо ймовірність події використавши нерівність Чебишева у такому вигляді. Знайти симетричний відносно М (Х) інтервал, що містить виміряне значення з ймовірністю р. Умови: Випадкова величина Х має нормальный закон розподілу з параметрами а=10, =5. Знайти а) Мат. Сподівання, б… Читати ще >
Завдання 4. Обчислення ймовірностей подій (реферат, курсова, диплом, контрольна)
Умови: Поданий закон розподілу випадкової величини Х.
Знайти а) Мат. Сподівання, б) дисперсію, в) середнє квадратичне відхилення.
Х. | ||||
Р. | 0,3. | 0,4. | 0,2. | 0,1. |
Розв’язок: Математичне сподівання розраховується за формулою.
А).

ймовірність математичний дисперсія А) M (X)=4*0,3+7*0,4+8*0,2+9*0,1=6,5.
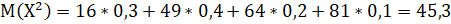
Б).

В).
Завдання 5
Умови:

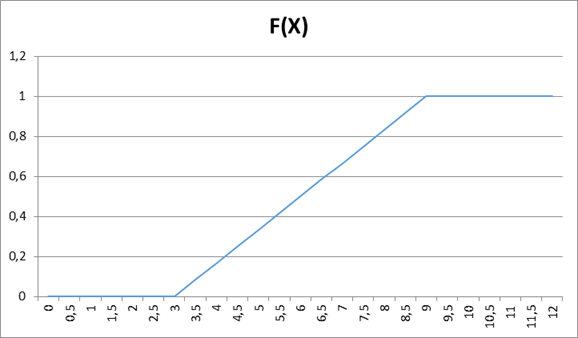
- 1) Знайти диференціальну функцію f (x)
- 2) Побудувати графіки F (x) і f (x)
- 3) Математичне сподівання X
- 4) Імовірність того, що Х прийме значення, належне до інтервалу (5;9)
а=3
в=9
с=5
d=9

Завдання 6
Умови: Задано щільність ймовірностей:


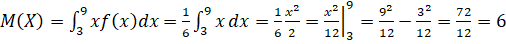
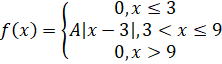
а=3, в=9.
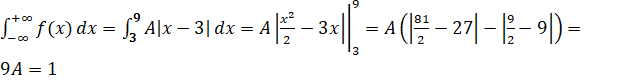
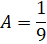
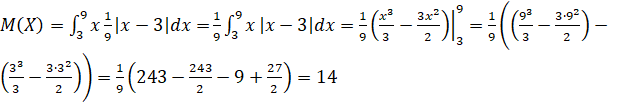

Мо=9.
Відповідь: А= М (x) = 14, D (x) =-67,(х) =.
Завдання7

Умови: Випадкова величина Х має нормальный закон розподілу з параметрами а=10, =5.
Знайти симетричний відносно М (Х) інтервал, що містить виміряне значення з ймовірністю р.
За умовою р=0,9588.
Розв’язок: Шуканий інтервал має вигляд.
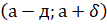

Значення знайдемо з умови.



=2,05.
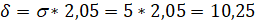
Відповідь: Інтервал, симетричний відносно М (х) має вигляд.
Завдання 8
Умови: Ймовірність появи випадкової події в кожній із 400 незалежних експериментів є величиною сталою і = р.
Використовуючи нерівність Чебишева оцінити ймовірність події.


якщо =10.
За умовою р=0,9588.
n=400; =10.
Розв’язок: Оцінимо ймовірність події використавши нерівність Чебишева у такому вигляді.
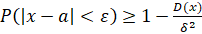
Відповідь: ймовірність події, якщо =10, а р=0,9588 = 0,158.