Критерій вибору пріоритету конкуруючих за ресурсами робіт при визначенні порядку їх виконання

Критерій вибору пріоритету конкуруючих за ресурсами робіт при визначенні порядку їх виконання Оптимізація сіткового графіка є процесом удосконалення організації виконання робіт програми з урахуванням термінів їх здачі. Заплановані заходи спрямовані на скорочення довжини критичного шляху, вирівнювання коефіцієнтів напруженості робіт, більш раціональне використання ресурсів.

Насамперед приймаються заходи, спрямовані на зменшення тривалості робіт критичного шляху: перерозподіл ресурсів усіх видів із резервних у критичні зони; зменшення трудомісткості критичних робіт за рахунок передачі частини робіт на шляхи з резервом часу; аналіз топології сітки; зміна складу робіт; введення паралельного виконання робіт критичного шляху. Процес скорочення тривалості виконання робіт може привести до утворення критичного шляху. У такому випадку слід перенести процес оптимізації на новий критичний шлях і так продовжувати до одержання ефективного варіанту. Виконання виробничої програми тісно пов’язане з вартісними чинниками виконання робіт. Вартісний фактор вводиться в сіткову модель шляхом визначення залежності «вартість-тривалість» для кожної роботи виробничої програми.

Точка В відповідає мінімальному режиму виконання роботи (i, j). Тривалість роботи в (i, j) можна зменшити, збільшивши інтенсивність використання ресурсів (тобто кількість ресурсів, витрачених на виконання роботи за одиницю часу), і як наслідок — вартість даної роботи зросте. Проте існує межа а (i, j), за якою подальше збільшення інтенсивності використання ресурсів призведе лише до збільшення затрат без скорочення тривалості робіт (точка А).

При цьому вартість С (i, j) роботи (i, j) прийме значення C (i, j) [Cmin (i, j);Cmax (i, j)], де Cmin (i, j) — вартість при максимальній тривалості роботи (i, j), C max (i, j) — вартість при мінімальній тривалості роботи (i, j).

Щоб провести криву, виконаємо апроксимацію по прямій і знайдемо зміну вартості роботи ДC (i, j) при скороченні її тривалості на величину [b (i, j)? t (i, j)]:

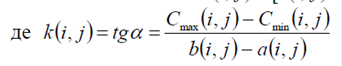
показує затрати на прискорення роботи (i, j) (у порівнянні з максимальною тривалістю) на одиницю часу; бкут нахилу апроксимованої прямої.

Проведемо оптимізаційний аналіз сіткового графіка з допомогою резервів часу робіт. Тривалість кожної роботи будемо збільшувати до тої пори, поки не буде використаним існуючий резерв часу, чи не буде досягнута верхня межа тривалості b (i, j).

У результаті, початкова вартість програми.

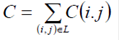
зменшиться на величину.

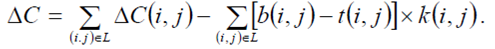
Задача 1.

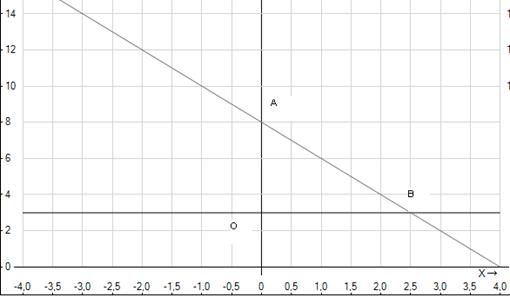
У задачах 1.5−1.14 знайти глобальний екстремум функції z в області рішень системи нерівностей.

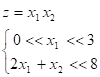
Розвязок. Область допустимих рішень — OAB. Лініями рівня є гіперболічна параболоїда. Глобальний мінімум знаходиться в точці O (0, 0). Максимальне значення цільова функція має в точці В (2,5, 3). Тому.

Відповідь. Глобальний максимум, дорівнює 7,5, досягається в точці В (2,5, 3), глобальний мінімум, дорівнює нулю, — в точці O (0, 0).

Задача 2.

Для задач 2.0−2.29 наведена таблиця 1, де вказані оцінки часу виконання робіт сітьового графіку, надані виконавцями та експертами.

Тривалість виконання роботи задається двома оцінками — мінімальна і максимальна. Мінімальна оцінка tmin (i, j) характеризує тривалість виконання роботи при найбільш сприятливих обставинах, а максимальна tmax (i, j) — при найбільш несприятливих умовах.

Тривалість роботи в цьому випадку розглядається, як випадкова величина, яка в результаті реалізації може прийняти будь-яке значення в заданому інтервалі. Такі оцінки називаються імовірнісними, і їх очікуване значення tоч (i, j) оцінюється за формулою:

tоч (i, j)=(3 tmin (i, j)+2 tmax (i, j))/5.

Для характеристики ступеня розкиду можливих значень навколо очікуваного рівня використовується показник дисперсії:

S2(i, j)=0,04(tmax (i, j)-tmin (i, j))2.

tоч (1,2)=(3*19+2*15)/5=16,6.

tоч (1,3)=(3*17+2*12)/5=14.

tоч (1,4)=(3*20+2*14)/5=16,4.

tоч (3,4)=(3*24+2*19)/5=21.

tоч (2,5)=(3*22+2*17)/5=19.

tоч (4,5)=(3*14+2*11)/5=12,2.

S2(1,2)=0,04*(19−15)2=0,64.

S2(1,3)=0,04*(17−12)2=1.

S2(1,4)=0,04*(20−14)2=1,44.

S2(3,4)=0,04*(24−19)2=1.

S2(2,5)=0,04*(24−19)2=1.

S2(4,5)=0,04*(14−11)2=0,36.

Розрахуємо очікуване значення і показник дисперсії.

Використовуючи отримані дані, ми можемо знайти основні характеристики сітьової моделі табличним методом, критичний шлях і його тривалість.

Перелік робіт та їх тривалість перенесемо в другу і третю графи. При цьому роботи слід записувати в графу 2 послідовно: спочатку починаючи з номера 1, потім з номера 2 і т.д.

У другій графі поставимо число, що характеризує кількість безпосередньо попередніх робіт (КПР) тієї події, з якого починається розглянута робота.

Так, для роботи (4,5) до графи 1 поставимо число 2, т.к. на номер 4 закінчуються 2 роботи: (1,4), (3,4).

Далі заповнюємо графи 4 і 5. Для робіт, що мають цифру 0 в графі 2, в графу 4 також заносяться нулі, а їх значення у графі 5 виходять в результаті підсумовування граф 3 і 4.

Для заповнення наступних рядків графи 4, тобто рядків починаючи з номера 2, проглядаються заповнені рядки графи 5, що містять роботи, які закінчуються на цей номер, і максимальне значення переноситься в графу 4 оброблюваних рядків.

Цей процес повторюється до тих пір, поки не буде заповнена остання рядок таблиці.

Заповнення графи 4. Графи 6 і 7 заповнюються зворотним ходом, тобто знизу вгору. Для цього проглядаються рядки, що закінчуються на номер останньої події, і з графи 5 вибирається максимальна величина, яка записується в графу 7 по всіх рядках, що закінчується на номер останньої події.

Процес повторюється до тих пір, поки не будуть заповнені всі рядки по графах 6 і 7.

Заповнення графи 7. Вміст графи 8 дорівнює різниці граф 6 і 4 або граф 7 і 5.

• а) графи 1 і 3 заповнюються на основі вихідних даних.
• б) у графі 2 записується кількість попередніх робіт по сітьовому графіку або визначається з графи 1 по числу робіт, що мають другою цифрою в коді ту, з якої починається дана робота.
• г) у графі 4 ранній початок робіт, що виходять з вихідного події, а раннє закінчення цих робіт одно їх тривалості (гр. 5). Ранній початок подальших робіт визначається шляхом вибору максимального з термінів раннього закінчення попередніх робіт. Кількість порівнюваних термінів дорівнює кількості попередніх робіт графи 2. Ранній початок подальших робіт можна визначити після того, як знайдено раннє закінчення попередніх. У свою чергу раннє закінчення кожної роботи знаходиться як сума величин раннього початку і тривалості даної роботи;
• г) тривалість критичного шляху визначається після заповнення граф 4 і 5 як максимальна величина з термінів раннього закінчення робіт, які ведуть до завершального події 9;
• д) знайдена величина критичного шляху ТKP днях заноситься в графу 7 для всіх робіт, що ведуть до завершального події. Потім заповнення ведеться знизу вгору. Знаходяться всі роботи, наступні за розглянутій, і визначаються різниці між пізнім закінченням цих робіт і їх тривалість. Мінімальна з величин заноситься в графу 7;
• е) у графі 6 пізній початок роботи визначається як різниця пізнього закінчення цих робіт та їх тривалості (із значень графи 7 віднімаються дані графи 3);
• ж) у графі 8 повний резерв часу роботи визначається різницею між значеннями граф 7 і 5. Якщо він дорівнює нулю, то робота є критичною;
• з) у графі 10 резерв часу подій j визначається як різниця пізнього закінчення роботи, який спливає подією j графи 7, і раннім початком роботи, начинающимся подією j;

і) значення вільного резерву часу роботи визначається як різниця значень графи 10 і даних графи 8 і вказує на розташування резервів, необхідних для оптимізації.

Критичний шлях: (1,3) (3,4) (4,5).

Тривалість критичного шляху: 47.2.

Для оцінки ймовірності виконання всього комплексу робіт за 25 днів нам необхідна наступна формула:

P (tкр < T) = 0,5 + 0,5Ф (Z).

де.

Z=(Т-Ткр)/Sкр

Z-нормативне відхилення випадкової величини,.

Sкр — середньоквадратичне відхилення, що обчислюється як корінь квадратний з дисперсії тривалості критичного шляху.

Відповідність між Z і Ф (Z) представлено в таблиці.

Критичний шлях проходить по роботах (1,3) (3,4) (4,5). Дисперсія критичного шляху:

S2(Lкр) = S2(1,3)+ S2(3,4)+ S2(4,5)=2.37.

S (Lкр) = 1.54.

Для вирішення поставленого завдання знайдемо значення аргументу Z, яке відповідає заданої ймовірності 95% (значенню графи Ф (Z) 0.95 * 100% в таблиці відповідає Z = 1.96).

Для визначення максимально можливого терміну виконання всього комплексу робіт з надійністю 95% будемо використовувати наступну формулу:

T = Ткр + Z * Sкр Для вирішення поставленого завдання знайдемо значення аргументу Z, яке відповідає заданої ймовірності 95% (значенню графи Ф (Z) 0,9545 * 100% в таблиці 5 відповідає Z = 1,96).

T = 47,2 +1,96 * 1,54 = 50,2.

Максимальний термін виконання всього комплексу робіт при заданому рівні ймовірності 95% становить всього 50,2 дня.

сітковий оптимізація вартісний Задача 3.

Попит кожного дня на деякий продукт складає 110 од. Витрати на покупку кожної партії цього продукту, які не залежать від об'єму партії, дорівнюють 1100 грошових одиниць, а витрати на зберігання одиниці продукту — 0.22 грошових одиниць за добу.

• 1) визначити найбільш економічний об'єм партії і інтервал між поставками партій такого об'єму;
• 2) визначити найбільш економічний об'єм партії і інтервал між поставками партій такого об'єму, при умові, що можливий дефіцит, який приносить 0.22 грошових одиниць збитку на добу за одиницю продукту.
• 1. Розрахунок найбільш економічного об'єму партії за формулою Вільсона:

где q0 — найбільш економічного об'єму партії, од.;

С1 — витрати на покупку кожної партії продукту, грошових одиниць.;

Q — попит кожного дня на продукт, шт.;

C2 — витрати на зберігання одиниці продукту, грошових одиниць за добу.

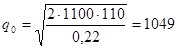
од.

Інтервал часу між замовленнями при умові дотримання оптимальної партії постачання.

.

де N — кількість робочих днів у році;

n — кількість партій поставок за період (рік);

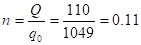
2. Найбільш економічний об'єм партії для задач с дефіцитом і без дефіцита при одинакових параметрах связані співвідношенням.

.

де.

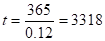
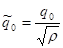
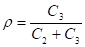
С3 = 0,22 — на штраф через дефіцит.

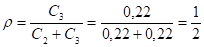
од.

Інтервал часу між замовленнями при умові дотримання оптимальної партії постачання.

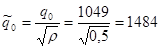
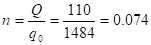
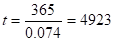
Список використаної літератури.

• 1. Бартіш М. Я. Методи оптимізації: Навч. посібник. — Львів: Видавничий центр ЛНУ імені Івана Франка, 2006.
• 2. Вентцель Е. С. Исследование операций. Задачи, принципы, методология: Учеб. пособие для вузов. — М.: Дрофа, 2004.
• 3. Волков И. К., Загоруйко Е. А. Исследование операций: Учебник. — М.: Изд-во МГТУ им. Н. Э. Баумана, 2002.
• 4. Зайченко Ю. П. Дослідження операцій: Підручник. — К.: ЗАТ «ВІПОЛ», 2000.
• 5. Зайченко Ю. П. Исследование операций: Учеб. пособие. — К.: Вища школа, 1975.
• 6. Катренко А. В. Дослідження операцій: Підручник. — Львів: Магнолія Плюс, 2004.
• 7. Костевич Л. С. Математическое программирование: Информ. технологии оптимальных решений: Учеб. пособие. — Мн.: Новое знание, 2003.
• 8. Кремер Н. Ш., Путко Б. А., Тришин И. М., Фридман М. Н. Исследование операций в экономике: Учеб. пособие. — М.: ЮНИТИ, 2004.
• 9. Ларичев О. И. Теория и методы принятия решений, а также Хроника событий в Волшебных странах: Учебник. — М.: Логос, 2003.
• 10. Машина Н. І. Математичні методи в економіці: Навч. посібник. — К.: Центр навчальної літератури, 2003.